题目内容
 (2011?上饶二模)如图所示,在空间中存在垂直纸面向里的场强为B匀强磁场,其边界AB、CD的宽度为d,在左边界的Q点处有一质量为m,带电量为负q的粒子沿与左边界成30°的方向射入磁场,粒子重力不计.求:
(2011?上饶二模)如图所示,在空间中存在垂直纸面向里的场强为B匀强磁场,其边界AB、CD的宽度为d,在左边界的Q点处有一质量为m,带电量为负q的粒子沿与左边界成30°的方向射入磁场,粒子重力不计.求:(1)带电粒子能从AB边界飞出的最大速度?
(2)若带电粒子能垂直CD边界飞出磁场,穿过小孔进入如图所示的匀强电场中减速至零且不碰到负极板,则极板间电压多大?
(3)若带电粒子的速度是
| 2dqB | m |
分析:(1)先作出粒子运动的轨迹,根据几何关系求出粒子能从左边界射出时临界情况的轨道半径,根据洛伦兹力提供向心力公式即可求解速度;
(2)同理求出粒子能从右边界射出时的半径,根据洛伦兹力提供向心力公式求解速度,根据动能定理求解极板间电压;
(3)根据速度求出粒子运动的半径,根据几何关系即可求得范围.
(2)同理求出粒子能从右边界射出时的半径,根据洛伦兹力提供向心力公式求解速度,根据动能定理求解极板间电压;
(3)根据速度求出粒子运动的半径,根据几何关系即可求得范围.
解答:解:(1)粒子能从左边界射出,临界情况有R+Rcos30°=d
Bqv=m
v=
=
所以粒子能从左边界射出速度应满足v≤
所以最大速度为
(2)粒子能从右边界射出
R=
Bqv2=m
m
=qU
解得U=
=
粒子不碰到右极板所加电压满足的条件 U≥
(3)当粒子速度为是
时 则R′=
,解得 R′=2d粒子,
若粒子沿OA方向射出,则会打在C点,根据几何关系可知:C点到O点在CD方向上的范围为l1=
d
粒子斜向下与右边界垂直方向成30°角射入时,刚好打在CD边界上,角度再大就不能打在右边界上了,根据几何关系可知l2=
d
所以范围为:l=l1+l2=2
d

答:(1)带电粒子能从AB边界飞出的最大速度为
;
(2)若带电粒子能垂直CD边界飞出磁场,穿过小孔进入如图所示的匀强电场中减速至零且不碰到负极板,则极板间电压满足U≥
;
(3)若带电粒子的速度是
,并可以从Q点沿纸面各个方向射入磁场,则粒子能打到CD边界的范围为2
d.
Bqv=m
| v2 |
| R |
v=
| Bqd |
| m(1+cos30°) |
2(2-
| ||
| m |
所以粒子能从左边界射出速度应满足v≤
2(2-
| ||
| m |
所以最大速度为
2(2-
| ||
| m |
(2)粒子能从右边界射出
R=
| d |
| cos30° |
Bqv2=m
| ||
| R |
| 1 |
| 2 |
| v | 2 2 |
解得U=
| B2qd2 |
| 2mcos230° |
| 2B2qd2 |
| 3m |
粒子不碰到右极板所加电压满足的条件 U≥
| 2B2qd2 |
| 3m |
(3)当粒子速度为是
| 2dqB |
| m |
| mv |
| Bq |
若粒子沿OA方向射出,则会打在C点,根据几何关系可知:C点到O点在CD方向上的范围为l1=
| 3 |
粒子斜向下与右边界垂直方向成30°角射入时,刚好打在CD边界上,角度再大就不能打在右边界上了,根据几何关系可知l2=
| 3 |
所以范围为:l=l1+l2=2
| 3 |

答:(1)带电粒子能从AB边界飞出的最大速度为
2(2-
| ||
| m |
(2)若带电粒子能垂直CD边界飞出磁场,穿过小孔进入如图所示的匀强电场中减速至零且不碰到负极板,则极板间电压满足U≥
| 2B2qd2 |
| 3m |
(3)若带电粒子的速度是
| 2dqB |
| m |
| 3 |
点评:带电粒子在磁场中的运动要把握其运动规律,在磁场中要注意找出相应的几何关系,从而确定圆心和半径,画出运动轨迹,难度适中.

练习册系列答案
相关题目
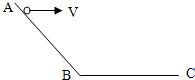 (2011?上饶二模)如图所示,AB为斜面,BC水平面.从A点以水平初速度v向右抛出一小球,其第一落点与A的水平距离为s1;从A点以水平初速度2v向右抛出一小球,其第一落点与A的水平距离为s2.不计空气阻力,则s1:s2可能为( )
(2011?上饶二模)如图所示,AB为斜面,BC水平面.从A点以水平初速度v向右抛出一小球,其第一落点与A的水平距离为s1;从A点以水平初速度2v向右抛出一小球,其第一落点与A的水平距离为s2.不计空气阻力,则s1:s2可能为( ) (2011?上饶二模)一弹簧一端固定在倾角为370光滑斜面的底端,另一端拴住的质量m1=4kg的物块P,Q为一重物,已知Q的质量m2=8kg,弹簧的质量不计,劲度系数k=600N/m,系统处于静止,如右图所示.现给Q施加一个方向沿斜面向上的力F,使它从静止开始斜向上做匀加速运动,已知在前0.2s时间内,F为变力,0.2s以后,F为恒力.求力F的最大值与最小值.(g=10m/s2)
(2011?上饶二模)一弹簧一端固定在倾角为370光滑斜面的底端,另一端拴住的质量m1=4kg的物块P,Q为一重物,已知Q的质量m2=8kg,弹簧的质量不计,劲度系数k=600N/m,系统处于静止,如右图所示.现给Q施加一个方向沿斜面向上的力F,使它从静止开始斜向上做匀加速运动,已知在前0.2s时间内,F为变力,0.2s以后,F为恒力.求力F的最大值与最小值.(g=10m/s2) (2011?上饶二模)承载着我国载人飞船和空间飞行器交会对接技术的“天宫一号”将于2011年下半年发射,随后将发射“神舟八号”飞船并与“天宫一号”实现交会对接.从此以“天宫一号”为平台开展空间实验室的有关技术验证,假设“天宫一号”和“神舟八号”绕地球做匀速圆周运动轨道如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.“天宫一号”和“神舟八号”离地高度分别为h1、h2,运行周期分别为T1、T2,地球可视为质量分布均匀的球体,且忽略自转影响,引力常量为G,则以下说法正确的是( )
(2011?上饶二模)承载着我国载人飞船和空间飞行器交会对接技术的“天宫一号”将于2011年下半年发射,随后将发射“神舟八号”飞船并与“天宫一号”实现交会对接.从此以“天宫一号”为平台开展空间实验室的有关技术验证,假设“天宫一号”和“神舟八号”绕地球做匀速圆周运动轨道如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.“天宫一号”和“神舟八号”离地高度分别为h1、h2,运行周期分别为T1、T2,地球可视为质量分布均匀的球体,且忽略自转影响,引力常量为G,则以下说法正确的是( )