题目内容
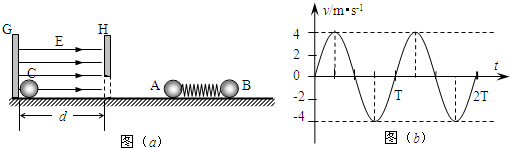
 如图(a)所示,一对平行光滑导轨放在水平面上,两导轨间的距离L=0.2米,导轨左端接一阻值为R=5Ω的电阻,有一导体杆静放在导轨上,杆与导轨垂直,杆与导轨的电阻不计.整个装置处在竖直向下的磁感强度为B=5T的匀强磁场中,当导体杆受到图(b)所示的水平向右的力F作用时,杆恰能做初速度为零的匀加速运动.求:
如图(a)所示,一对平行光滑导轨放在水平面上,两导轨间的距离L=0.2米,导轨左端接一阻值为R=5Ω的电阻,有一导体杆静放在导轨上,杆与导轨垂直,杆与导轨的电阻不计.整个装置处在竖直向下的磁感强度为B=5T的匀强磁场中,当导体杆受到图(b)所示的水平向右的力F作用时,杆恰能做初速度为零的匀加速运动.求:(1)杆在F作用下的加速度和杆的质量;
(2)在0-10s内电阻R上流过的电量;
(3)若在10s后撤去F,则此后电阻R上产生的热量;
(4)若在10s末F变为恒力,且此恒力与10s末相同,那么导体杆将如何运动?
分析:(1)根据法拉第电磁感应定律、欧姆定律、安培力公式和速度公式推导出安培力与时间的关系式,由牛顿第二定律得出加速度与时间的关系式,由数学知识分析图线的斜率与截距的意义,求解加速度和杆的质量;
(2)由位移公式求出在0-10s内导体杆的位移,由电磁感应定律、欧姆定律、电流公式得到电量.
(3)由速度公式求出10s末导体杆的速度,根据能量守恒定律求出热量.
(4)分析安培力的变化,判断导体杆的运动情况.
(2)由位移公式求出在0-10s内导体杆的位移,由电磁感应定律、欧姆定律、电流公式得到电量.
(3)由速度公式求出10s末导体杆的速度,根据能量守恒定律求出热量.
(4)分析安培力的变化,判断导体杆的运动情况.
解答:解:(1)由E=BLv,I=
,F安=BIL得,安培力大小F安=
,根据牛顿第二定律得,
F-F安=ma,
则有F-
=ma,F=
+ma=
+ma,
由数学知识可知,图线的斜率k=
,纵轴的截距等于ma.
由图得到k=
=0.04,ma=0.2,
代入解得,a=0.2m/s2,m=1kg.
(2)在0-10s内导体杆通过的位移为x=
at2=10m,
电阻R上流过的电量q=
=
=2C;
(3)在10s末导体杆的速度为v=at=0.2×10m/s=2m/s.
在10s后撤去F,导体杆做减速运动直到停止运动,
根据能量守恒得,电阻R上产生的热量Q=
mv2=2J;
(4)若在10s末F变为恒力后,安培力逐渐增大,加速度逐渐减小,导体杆先变加速运动,当安培力与恒力平衡时,导体杆做匀速直线运动.
答:
(1)杆在F作用下的加速度和杆的质量分别为a=0.2m/s2,m=1kg.
(2)在0-10s内电阻R上流过的电量是2C;
(3)若在10s后撤去F,此后电阻R上产生的热量是2J;
(4)若在10s末F变为恒力,且此恒力与10s末相同,导体杆将导体杆先变加速运动,最后做匀速直线运动.
| E |
| R |
| B2L2v |
| R |
F-F安=ma,
则有F-
| B2L2v |
| R |
| B2L2v |
| R |
| B2L2at |
| R |
由数学知识可知,图线的斜率k=
| B2L2a |
| R |
由图得到k=
| 0.6-0.2 |
| 10 |
代入解得,a=0.2m/s2,m=1kg.
(2)在0-10s内导体杆通过的位移为x=
| 1 |
| 2 |
电阻R上流过的电量q=
| △Φ |
| R |
| BLx |
| R |
(3)在10s末导体杆的速度为v=at=0.2×10m/s=2m/s.
在10s后撤去F,导体杆做减速运动直到停止运动,
根据能量守恒得,电阻R上产生的热量Q=
| 1 |
| 2 |
(4)若在10s末F变为恒力后,安培力逐渐增大,加速度逐渐减小,导体杆先变加速运动,当安培力与恒力平衡时,导体杆做匀速直线运动.
答:
(1)杆在F作用下的加速度和杆的质量分别为a=0.2m/s2,m=1kg.
(2)在0-10s内电阻R上流过的电量是2C;
(3)若在10s后撤去F,此后电阻R上产生的热量是2J;
(4)若在10s末F变为恒力,且此恒力与10s末相同,导体杆将导体杆先变加速运动,最后做匀速直线运动.
点评:此题中用到电磁感应现象中常用的两个经验公式:安培力F安=
,感应电量q=n
,要在理解的基础上记牢,并能灵活应用.
| B2L2v |
| R |
| △Φ |
| R |

练习册系列答案
相关题目