题目内容
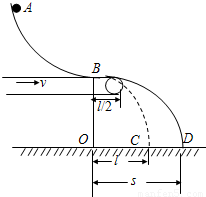 如图所示,AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平.一个质量为m的小物体P从轨道顶端A处由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示,已知它落地时相对于B点的水平位移OC=l.现在轨道下方紧贴B点安装一水平传送带,传送带的右端与B的距离为l/2.当传送带静止时,让 P再次从A点由静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落在地面的C点,当驱动转动带动传送带以速度v匀速向右运动时(其他条件不变),P的落地点为 D.不计空气阻力.
如图所示,AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平.一个质量为m的小物体P从轨道顶端A处由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示,已知它落地时相对于B点的水平位移OC=l.现在轨道下方紧贴B点安装一水平传送带,传送带的右端与B的距离为l/2.当传送带静止时,让 P再次从A点由静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落在地面的C点,当驱动转动带动传送带以速度v匀速向右运动时(其他条件不变),P的落地点为 D.不计空气阻力.a)求P滑到B点时的速度大小
b)求P与传送带之间的摩擦因数
c)求出O、D间的距离s 随速度v变化的函数关系式.
【答案】分析:a)AB是光滑轨道,物体P从轨道顶端处A点滑到B点过程机械能守恒,由机械能守恒定律求出物体P滑到B的速度大小.
b)根据动能定理研究物体P在传送带上滑行过程,求出动摩擦因数;
c)通过物体P滑到底端的速度与传送带的速度进行比较,判断物体P在传送带上的运动情况,得出物体离开传送带的速度,根据平抛运动的知识求出水平位移.
解答:解:a)根据机械能守恒定律有: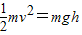 ,
,
解得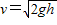 .
.
b)在两种情况下物体P在空中的运动时间相同,位移分别为:x=l,x1= .
.
∴v1=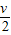 =
=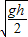 .
.
根据动能定理有-μmg =
=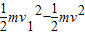 .
.
解得μ=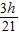 .
.
c)平抛运动的时间t=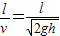 .
.
若v≤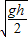 时,P一直做匀减速直线运动,到达传送带右端的速度等于
时,P一直做匀减速直线运动,到达传送带右端的速度等于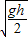 ,所以平抛运动的水平位移s=l.
,所以平抛运动的水平位移s=l.
若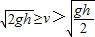 时,P先做匀减速直线运动,后做匀速直线运动,到达传送带右端的速度等于v,所以s=vt=
时,P先做匀减速直线运动,后做匀速直线运动,到达传送带右端的速度等于v,所以s=vt=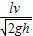 .
.
若P一直做匀加速直线运动,根据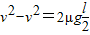 ,解得v=
,解得v=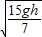 ,若
,若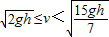 ,则P先做匀加速直线运动,再做匀速直线运动,到达传送带右端的速度等于v,所以s=vt=
,则P先做匀加速直线运动,再做匀速直线运动,到达传送带右端的速度等于v,所以s=vt=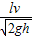 .
.
若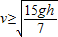 ,则P一直做匀加速直线运动,到达传送带右端的速度为
,则P一直做匀加速直线运动,到达传送带右端的速度为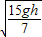 ,所以s=
,所以s=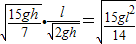 .
.
答:(1)P滑到B点时的速度大小为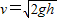 .
.
(2)P与传送带之间的摩擦因数为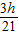 .
.
(3)当v≤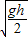 时,s=l.
时,s=l.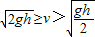 时,s=
时,s=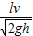 .当
.当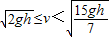 ,则s=
,则s=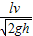 .当
.当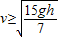 ,s=
,s=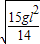 .
.
点评:本题是机械能守恒、平抛运动,动能定理的综合应用,要具有分析物体运动过程的能力,要抓住平抛运动的时间由高度决定这一知识点.
b)根据动能定理研究物体P在传送带上滑行过程,求出动摩擦因数;
c)通过物体P滑到底端的速度与传送带的速度进行比较,判断物体P在传送带上的运动情况,得出物体离开传送带的速度,根据平抛运动的知识求出水平位移.
解答:解:a)根据机械能守恒定律有:
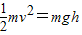 ,
,解得
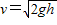 .
.b)在两种情况下物体P在空中的运动时间相同,位移分别为:x=l,x1=
 .
.∴v1=
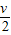 =
=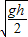 .
.根据动能定理有-μmg
 =
=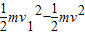 .
.解得μ=
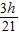 .
.c)平抛运动的时间t=
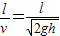 .
.若v≤
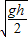 时,P一直做匀减速直线运动,到达传送带右端的速度等于
时,P一直做匀减速直线运动,到达传送带右端的速度等于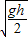 ,所以平抛运动的水平位移s=l.
,所以平抛运动的水平位移s=l.若
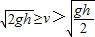 时,P先做匀减速直线运动,后做匀速直线运动,到达传送带右端的速度等于v,所以s=vt=
时,P先做匀减速直线运动,后做匀速直线运动,到达传送带右端的速度等于v,所以s=vt=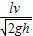 .
.若P一直做匀加速直线运动,根据
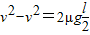 ,解得v=
,解得v=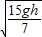 ,若
,若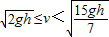 ,则P先做匀加速直线运动,再做匀速直线运动,到达传送带右端的速度等于v,所以s=vt=
,则P先做匀加速直线运动,再做匀速直线运动,到达传送带右端的速度等于v,所以s=vt=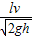 .
.若
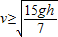 ,则P一直做匀加速直线运动,到达传送带右端的速度为
,则P一直做匀加速直线运动,到达传送带右端的速度为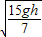 ,所以s=
,所以s=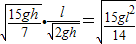 .
.答:(1)P滑到B点时的速度大小为
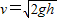 .
.(2)P与传送带之间的摩擦因数为
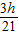 .
.(3)当v≤
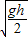 时,s=l.
时,s=l.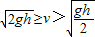 时,s=
时,s=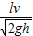 .当
.当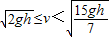 ,则s=
,则s=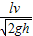 .当
.当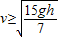 ,s=
,s=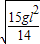 .
.点评:本题是机械能守恒、平抛运动,动能定理的综合应用,要具有分析物体运动过程的能力,要抓住平抛运动的时间由高度决定这一知识点.

练习册系列答案
相关题目
 如图所示,AB是一段质量分布不均匀的棒.两次将棒靠在光滑的竖直墙壁和粗糙的水平地面之间,棒处于静止状态,一次是A端在上,一次是B端在上,两次棒与地面的夹角可视为相同,两次相比较,则有( )
如图所示,AB是一段质量分布不均匀的棒.两次将棒靠在光滑的竖直墙壁和粗糙的水平地面之间,棒处于静止状态,一次是A端在上,一次是B端在上,两次棒与地面的夹角可视为相同,两次相比较,则有( ) 某同学设计了一个测定列车加速度的仪器,如图所示.AB是一段圆弧形的电阻,O点为其圆心,圆弧半径为r.O点下用一电阻不计的金属线悬挂着一个金属球,球的下部与AB接触良好且无摩擦.A、B之间接有内阻不计、电动势为9V的电池,电路中接有理想电流表A,O、B间接有一个理想电压表V.整个装置在一竖直平面内,且装置所在平面与列车前进的方向平行.下列说法中正确的有( )
某同学设计了一个测定列车加速度的仪器,如图所示.AB是一段圆弧形的电阻,O点为其圆心,圆弧半径为r.O点下用一电阻不计的金属线悬挂着一个金属球,球的下部与AB接触良好且无摩擦.A、B之间接有内阻不计、电动势为9V的电池,电路中接有理想电流表A,O、B间接有一个理想电压表V.整个装置在一竖直平面内,且装置所在平面与列车前进的方向平行.下列说法中正确的有( ) (2008?广东模拟)如图所示,ab是一段弯管,其中心线是半径为R的圆弧,弯管平面与匀强磁场方向垂直,一束质量、速率各不相同的一价正离子(不计重力),对准a端射入弯管,则可以沿中心线穿过的离子必定是( )
(2008?广东模拟)如图所示,ab是一段弯管,其中心线是半径为R的圆弧,弯管平面与匀强磁场方向垂直,一束质量、速率各不相同的一价正离子(不计重力),对准a端射入弯管,则可以沿中心线穿过的离子必定是( ) (2009?虹口区一模)某同学设计了一个测定列车加速度的仪器,如图所示.AB是一段圆弧形的电阻,O点为其圆心,圆弧半径为r.O点下用一电阻不计的金属线悬挂着金属球,球的下部与AB接触良好且无摩擦.AB之间接有内阻不计、电动势为9V的电池,OB间接有一个伏特表.整个装置的竖直面沿列车前进的方向放置.当列车做匀加速运动,悬线就偏过一定角度.若伏特表显示3V,则列车的加速度为
(2009?虹口区一模)某同学设计了一个测定列车加速度的仪器,如图所示.AB是一段圆弧形的电阻,O点为其圆心,圆弧半径为r.O点下用一电阻不计的金属线悬挂着金属球,球的下部与AB接触良好且无摩擦.AB之间接有内阻不计、电动势为9V的电池,OB间接有一个伏特表.整个装置的竖直面沿列车前进的方向放置.当列车做匀加速运动,悬线就偏过一定角度.若伏特表显示3V,则列车的加速度为
 g
g