题目内容
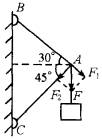
由轻杆组成的三角支架用绞链固定在竖直墙上,如图所示,轻杆AC只能承受压力2000N,AB杆只能承受拉力1000N,要使支架不损坏,在A点悬挂的重物重量最多为多少?

图
答案:
解析:
提示:
解析:
先假设AC杆所受压力为2000N,计算AB杆此时承受的拉力,若比1000N大,则AB杆先断,只要AB杆不断,支架就很安全;若比1000N小,则AC杆先断,只要AC杆不断,支架就安全. 在支架的A端悬挂重物后,由于AB、AC都是轻杆,B、C又是绞链连接,因此作用在杆上的力应沿杆的方向,支架A端因挂重物产生的拉力F产生两个实际效果:拉AB杆,压AC杆,将F(F=G)沿这两个方向分解,作出平行四边形如图中虚线所画,从图中可以看出,力构成的矢量三角形和支架组成的三角形相似,根据三角形的正弦定理可得
即 若F2=2000N时
杆AB会拉断 若F1=1000N时,F2 两杆都不会损坏,所以以F1=1000N进行运算
得F=500( 因F=G,故在A点悬挂的重物重量最多不能超过500(
|
提示:
此题用力的分解的方法求解,也可把A点受力正交分解,用共点力平衡的方法求解,在解答过程中,可灵活采用不同的数学方法,如三角形相似比例法、正弦定理、余弦定理等.
|

练习册系列答案
相关题目