题目内容
如图所示,两个完全相同的弹性小球A和B分别挂在l和l/4的细线上,重心在同一水平面且小球恰好相互接触,把第一个小球A向右拉开一个不大的距离后由静止释放,经过多长时间两球发生第12次碰撞(两球碰撞时交换速度)?
【答案】分析:由于两球相撞时交换速度,则球1从最大位移处摆下来碰静止的球2后,球1静止,球2运动.同样,球2摆下来碰静止的球1后,球2静止,球1运动.所以,总是只有一个球在摆动,两球总是在最低点相碰.
解答:解:球A运动的周期TA=2π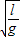 ,
,
球B运动的周期TB=2π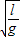 =π
=π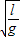 .
.
则该振动系统的周期
T= TA+
TA+ TB=
TB= (TA+TB)=
(TA+TB)=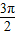
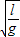 .
.
在每个周期T内两球会发生两次碰撞,球A从最大位移处由静止开始释放后,经6T=9π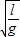 ,发生12次碰撞,且第12次碰撞后A球又回到最大位置处所用时间为t′=
,发生12次碰撞,且第12次碰撞后A球又回到最大位置处所用时间为t′=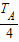 .
.
所以从释放A到发生第12次碰撞所用时间为
t=6T-t′=9π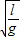 -
-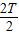
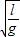 =
=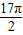
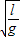 .
.
答:经过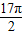
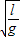 两球发生第12次碰撞.
两球发生第12次碰撞.
点评:本题考查了单摆的周期公式,解决本题的关键是知道两个摆总是一个在动,理解系统的周期.
解答:解:球A运动的周期TA=2π
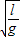 ,
,球B运动的周期TB=2π
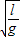 =π
=π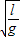 .
.则该振动系统的周期
T=
 TA+
TA+ TB=
TB= (TA+TB)=
(TA+TB)=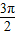
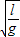 .
.在每个周期T内两球会发生两次碰撞,球A从最大位移处由静止开始释放后,经6T=9π
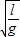 ,发生12次碰撞,且第12次碰撞后A球又回到最大位置处所用时间为t′=
,发生12次碰撞,且第12次碰撞后A球又回到最大位置处所用时间为t′=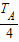 .
.所以从释放A到发生第12次碰撞所用时间为
t=6T-t′=9π
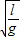 -
-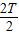
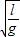 =
=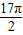
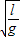 .
.答:经过
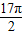
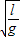 两球发生第12次碰撞.
两球发生第12次碰撞.点评:本题考查了单摆的周期公式,解决本题的关键是知道两个摆总是一个在动,理解系统的周期.

练习册系列答案
相关题目
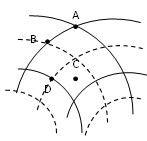
 (2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( ) (2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )