题目内容
 如图所示,一块质量均匀、水平放置的绝缘平板长2m,其左端A靠在竖直墙面上,中心C固定在高1m的支架上,支架下端与水平固定转轴O连接,平板可绕转动轴O沿顺时针方向翻转.在平板A点处有一质量为0.1kg的带正电小物体M以初速v0开始向右运动,物体与平板间的动摩擦因数μ=0.2.试求:
如图所示,一块质量均匀、水平放置的绝缘平板长2m,其左端A靠在竖直墙面上,中心C固定在高1m的支架上,支架下端与水平固定转轴O连接,平板可绕转动轴O沿顺时针方向翻转.在平板A点处有一质量为0.1kg的带正电小物体M以初速v0开始向右运动,物体与平板间的动摩擦因数μ=0.2.试求:(1)为使平板不翻倒,物体的初速v0的最大值.
(2)若物体所带电量q=10-5C,在整个空间加场强为E=3×104 N/C、水平向左的匀强电场,则为使平板不翻倒,物体的初速v0的最大值又可以为多少?
(3)与(2)条件相同,若物体的初速v0=2m/s,物体与墙面碰撞时能量不损失,则当物体最终停止时,运动的总路程为多少?
分析:(1)以平板为研究对象,以O转轴,当平板受到的M压力力矩与摩擦力力矩相等时,平板刚要翻倒,根据力矩平衡条件列式,求出平板不翻倒时M在平板上滑行的最大距离,由运动学公式和牛顿第二定律结合求出初速v0的最大值;
(2)根据牛顿第二定律求出物体的加速度,物体仍滑到上题位置时,平板刚要翻倒,由运动学公式求初速度.
(3)总路程与滑动摩擦力做功有关,对整个过程,运用动能定理求解总路程.
(2)根据牛顿第二定律求出物体的加速度,物体仍滑到上题位置时,平板刚要翻倒,由运动学公式求初速度.
(3)总路程与滑动摩擦力做功有关,对整个过程,运用动能定理求解总路程.
解答:解:(1)设为使平板不翻倒,物体向右滑行的最大距离为s.
平板刚要翻倒时,由力矩平衡条件得 mg(LAC-s)=μmgLOC
解得 s=0.8m
物体的加速度大小为a=
=μg=2m/s2
则 v0≤
=
m/s
(2)在整个空间加场强为E=3×104 N/C、水平向左的匀强电场时,物体受到了水平向左的电场力,此时加速度为a′=
=5m/s2
则v0′≤
=
m/s
(3)对于整个运动过程,运用动能定理得:
-μmgS总=0-
mv2
解得,S总=1m
答:
(1)为使平板不翻倒,物体的初速v0的最大值是
m/s.
(2)为使平板不翻倒,物体的初速v0的最大值又可以为
m/s.
(3)当物体最终停止时,运动的总路程为1m.
平板刚要翻倒时,由力矩平衡条件得 mg(LAC-s)=μmgLOC
解得 s=0.8m
物体的加速度大小为a=
| μmg |
| m |
则 v0≤
| 2as |
| 3.2 |
(2)在整个空间加场强为E=3×104 N/C、水平向左的匀强电场时,物体受到了水平向左的电场力,此时加速度为a′=
| μmg+qE |
| m |
则v0′≤
| 2a′s |
| 8 |
(3)对于整个运动过程,运用动能定理得:
-μmgS总=0-
| 1 |
| 2 |
解得,S总=1m
答:
(1)为使平板不翻倒,物体的初速v0的最大值是
| 3.2 |
(2)为使平板不翻倒,物体的初速v0的最大值又可以为
| 8 |
(3)当物体最终停止时,运动的总路程为1m.
点评:本题是力矩平衡条件、牛顿第二定律、运动学规律和动能定理的综合.当要求总路程时,往往根据滑动摩擦力做功与总路程有关,由动能定理求解.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图所示,一块质量为M,长为L的均质长木板放在很长的光滑水平桌面上,板的左端有一质量为m的小物体(可视为质点),物体上连接一根很长的细绳,细绳跨过位于桌边的定滑轮.某人以恒定的速率v向下拉绳,物体最多只能到达板的中点,已知整个过程板的右端都不会到达桌边定滑轮处.试求:
如图所示,一块质量为M,长为L的均质长木板放在很长的光滑水平桌面上,板的左端有一质量为m的小物体(可视为质点),物体上连接一根很长的细绳,细绳跨过位于桌边的定滑轮.某人以恒定的速率v向下拉绳,物体最多只能到达板的中点,已知整个过程板的右端都不会到达桌边定滑轮处.试求: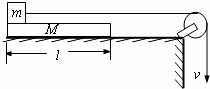 (2007?湖南模拟)如图所示,一块质量为M、长为l的匀质板放在很长的光滑水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮,某人以恒定的速度υ向下拉绳,物块最多只能到达板的中点,而且此时板的右端尚未到达桌边定滑轮.求:
(2007?湖南模拟)如图所示,一块质量为M、长为l的匀质板放在很长的光滑水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮,某人以恒定的速度υ向下拉绳,物块最多只能到达板的中点,而且此时板的右端尚未到达桌边定滑轮.求: 如图所示,一块质量为M=2kg,长为L的均质板静止在很长的光滑水平桌面上,板的左端静止摆放质量为m=1kg的小物体(可视为质点),M和m之间的为动摩擦因数为μ=0.2.在小物体m上的O点连接一根很长的轻质细绳,细绳跨过位于桌边的定滑轮.t=0s时刻某人以恒定拉力F=3.3N向下拉绳,t1=2s时刻细绳突然从O处断开,最后小物体m刚好能到长木板M的最右端(定滑轮光滑,长木板右端和定滑轮之间的距离足够长,g取10m/s2).求:
如图所示,一块质量为M=2kg,长为L的均质板静止在很长的光滑水平桌面上,板的左端静止摆放质量为m=1kg的小物体(可视为质点),M和m之间的为动摩擦因数为μ=0.2.在小物体m上的O点连接一根很长的轻质细绳,细绳跨过位于桌边的定滑轮.t=0s时刻某人以恒定拉力F=3.3N向下拉绳,t1=2s时刻细绳突然从O处断开,最后小物体m刚好能到长木板M的最右端(定滑轮光滑,长木板右端和定滑轮之间的距离足够长,g取10m/s2).求:
