Question

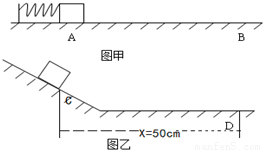
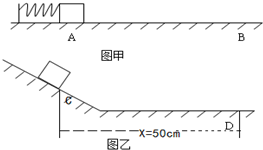如图甲，水平面上质量m=2kg的小物体被一根已压缩的弹簧自A点弹出，与弹簧分离后又滑行一段距离停止在B点．已知物体与水平面间的动摩擦因数μ=0.4，AB间距离X=50cm．（g=10m/s²）
（1）求弹簧释放的弹性势能．
（2）将水平面弯成如图乙的一部分斜面与一部分水平面的对接（对接处有很小的光滑圆弧过渡），将物体自斜面上C点由静止释放，物体滑下斜面后又在水平面上滑动一段距离并停止于D点．已知CD间的水平距离也为50cm．求C点距水平面的高度h．

Answer 1

分析：（1）在物体自A运动到B过程中，根据动能定理列式求出弹簧对物体做的功，弹簧释放的弹性势能等于弹簧对物体做的功；
（2）从C到D的整个过程运用动能定理列式即可求解．

解答：解：（1）在物体自A运动到B过程中，弹簧对物体做功设为W_F，摩擦做功为W_f
根据动能定理：W_F+W_f=0
根据功的公式：W_f=-μmgX
设弹簧释放的弹性势能为Ep，则Ep=W_F
可得Ep=4J
（2）设物体在斜面上滑动对应的水平距离为X₁，在水平面上对应的距离为X₂
X=X₁+X₂
物体自C运动到D过程中，重力做功设为W_G，摩擦在斜面上做功W₁，在水平面上做功W₂
根据动能定理：W_G+W₁+W₂=0
W_G=mgh    
W₁=-μmgX₁
W₂=-μmgX₂
得：h=0.2m
答：（1）求弹簧释放的弹性势能为4J．
（2）C点距水平面的高度为0.2m．

点评：本题主要考查了动能定理的直接应用，难度不大，属于基础题．