题目内容
某星球的质量为M，在该星球表面某一倾角为θ的山坡上以初速度vo平抛一物体，经时间t该物体落到山坡上．欲使该物体不再落回该星球的表面，求至少应以多大的速度抛出该物体？（不计一切阻力，万有引力常量为G）
分析：根据平抛运动规律列出水平方向和竖直方向的位移等式，结合几何关系求出重力加速度．
忽略地球自转的影响，根据万有引力等于重力列出等式．
若要使物体不再落后星球，应使物体绕着星球表面做匀速圆周运动，由万有引力定律充当向心力可求得抛出速度
忽略地球自转的影响，根据万有引力等于重力列出等式．
若要使物体不再落后星球，应使物体绕着星球表面做匀速圆周运动，由万有引力定律充当向心力可求得抛出速度
解答：解：由题意可知是要求该星球上的“近地卫星”的绕行速度，也即为第一宇宙速度．
设该星球表面处的重力加速度为g，
由平抛运动可得 tanθ=
=
①
故g=
对于该星球表面上的物体有
=mg ②
所以R=
而对于绕该星球做匀速圆周运动的“近地卫星”应有mg=
③
由 ①②③式得 v=
=
答：欲使该物体不再落回该星球的表面，至少应以
的速度抛出该物体．
设该星球表面处的重力加速度为g，
由平抛运动可得 tanθ=
| y |
| x |
| gt |
| 2v0 |
故g=
| 2v0tanθ |
| t |
对于该星球表面上的物体有
| GMm |
| R2 |
所以R=
|
而对于绕该星球做匀速圆周运动的“近地卫星”应有mg=
| mv2 |
| R |
由 ①②③式得 v=
| gR |
| 4 |
| ||
答：欲使该物体不再落回该星球的表面，至少应以
| 4 |
| ||
点评：处理平抛运动的思路就是分解．
重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量．
重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量．
练习册系列答案
相关题目
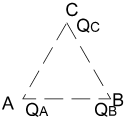静电场与引力场有着非常相似的性质，力的形式都遵从平方反比定律，解答下列问题：
时间该物体落到山坡上。欲使该物体不再落回该星球的表面，至少应以多大的速度抛出物体（不计一切阻力，万有引力常量为G）？