题目内容

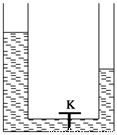
在图所示的两端开口的“U”形管中，盛有同种液体，并用阀门K将液体隔成左、右两部分，左边液面比右边液面高．现打开阀门K，从打开阀门到两边液面第一次平齐的过程中，液体向外放热为Q，内能变化量为ΔU，动能变化量为ΔE_k；大气对液体做功为W₁，重力做功为W₂，液体克服阻力做功为W₃，由功能关系可得

①W₁＝0 ②W₂－W₃＝ΔE_k

③W₂－W₃＝Q＝ΔU ④W₃－Q＝ΔU

其中，正确的是( )

A．①②③ B．①②④

C．②③ D．①③

【答案】

【解析】

试题分析：由动能定理可知W₂－W₃＋W₁＝ΔE_k，其中W₁＝p·ΔV_左－p·ΔV_右＝0，可知①、②正确．

由热力学第一定律ΔU＝W＋Q得ΔU＝W₃－Q，可知④正确，③错误．

综合以上分析可知B正确．

考点：本题考查了动能定理和热力学第一定律的应用

点评：能量守恒也适合于内能和宏观能量之间的转化与守恒，所以熟练掌握热力学第一定律是进一步理解能量守恒与转化。

练习册系列答案

在图所示的两端开口的“U”形管中，盛有同种液体，并用阀门K将液体隔成左、右两部分，左边液面比右边液面高．现打开阀门K，从打开阀门到两边液面第一次平齐的过程中，液体向外放热为Q，内能变化量为ΔU，动能变化量为ΔE_k；大气对液体做功为W₁，重力做功为W₂，液体克服阻力做功为W₃，由功能关系可得

①W₁＝0 ②W₂-W₃＝ΔE_k
③W₂-W₃＝Q＝ΔU ④W₃-Q＝ΔU
其中，正确的是

A.
①②③
B.
①②④
C.
②③
D.
①③

某研究性学习小组发现河水在缓慢流动时有一个规律，河中央流速最大，岸边速度几乎为零．为了研究河水流速与从岸边到中央距离的关系，小明同学设计了这样的测量仪器：如图甲所示，两端开口的“L”型玻璃管的水平部分置于待测的水流中，竖直部分露出水面，且露出水面部分的玻璃管足够长．当水流以速度 v 正对“L”型玻璃管的水平部分开口端匀速流动时，管内外液面的高度差为 h，且h 随水流速度的增大而增大．为了进一步研究水流速度v 与管内外水面高度差h的关系，该组同学进行了定量研究，得到了如下的实验数据，并根据实验数据得到了v-h 图象，如图丙所示．

v（m/s） 0 1.00 1.41 1.73 2.00 2.45 3.00 3.16
h（m） 0 0.05 0.10 0.15 0.20 0.30 0.45 0.50
（1）根据根据上表的数据和图丙中图象的形状，可猜想v和h之间的关系为；为验证猜，请在图丁中确定纵轴所表示的物理量，并另作图象，若该图象的形状为，说明猜想正确．

（2）现利用上述测速器，由河流南岸开始，每隔1米测一次流速，得到数据如下表所示：
测试点距岸距离 x/m 0 1 2 3 4 5 6
管内外高度差　 h/cm 0 0.8 3.2 7.2 12.8 20.0 28.8
相应的水流速度 v/ms^-1
根据v和h之间的关系完成上表的最后一行，对比上表中的数据，可以看出河中水流速度 v 与从南岸到河流中央距离x的关系为：．

（08年厦门双十中学月考）（10分）某研究性学习小组发现河水在缓慢流动时有一个规律，河中央流速最大，岸边速度几乎为零。为了研究河水流速与离河岸距离的关系，小明设计了这样的测量仪器：如图甲所示，两端开口的“L”形玻璃管的水平部分置于待测的水流中，竖直部分露出水面，且露出水面部分的玻璃管足够长。当水流以速度v正对“L”形玻璃管的水平部分开口端匀速流动时，管内外水面高度差为h，且h随水流速度的增大而增大。为了进一步研究水流速度v与管内外水面高度差h的关系，该组同学进行了定量研究，得到了如下表所示的实验数据，并根据实验数据得到了v-h图像，如图丙所示。

v（m/s）	0	1.00	1.41	1.73	2.00	2.45	2.83	3.16
h（m）	0	0.05	0.10	0.15	0.20	0.30	0.40	0.50

（1）根据上表的数据和图丙中图像的形状，可猜想v和h之间的关系为；为验证猜想，请在图丁中确定纵轴所表示的物理量，并作出图像，若该图像的形状为，说明猜想正确。

（2）现利用上述测速器，由河流南岸开始，每隔1 m测一次流速，得到数据如下表所示：根据v和h之间的关系完成下表的最后一行，对比下表中的数据，可以看出河中水流速度v与离南岸的距离x的关系为。

测试点离岸距离x/m	0	1	2	3	4
管内外液面高度差h/cm	0	0.8	3.2	7.2	12.8
相应的河水流速v/ms^-1

第六部分振动和波

第一讲基本知识介绍

《振动和波》的竞赛考纲和高考要求有很大的不同，必须做一些相对详细的补充。

一、简谐运动

1、简谐运动定义：= －k ①

凡是所受合力和位移满足①式的质点，均可称之为谐振子，如弹簧振子、小角度单摆等。

谐振子的加速度：= －

2、简谐运动的方程

回避高等数学工具，我们可以将简谐运动看成匀速圆周运动在某一条直线上的投影运动（以下均看在x方向的投影），圆周运动的半径即为简谐运动的振幅A 。

依据：_x = －mω²Acosθ= －mω²

对于一个给定的匀速圆周运动，m、ω是恒定不变的，可以令：

mω² = k

这样，以上两式就符合了简谐运动的定义式①。所以，x方向的位移、速度、加速度就是简谐运动的相关规律。从图1不难得出——

位移方程： = Acos(ωt + φ) ②

速度方程： = －ωAsin(ωt +φ) ③

加速度方程：= －ω²A cos(ωt +φ) ④

相关名词：(ωt +φ)称相位，φ称初相。

运动学参量的相互关系：= －ω²

A =

tgφ= －

3、简谐运动的合成

a、同方向、同频率振动合成。两个振动x₁ = A₁cos(ωt +φ₁)和x₂ = A₂cos(ωt +φ₂) 合成，可令合振动x = Acos(ωt +φ) ，由于x = x₁ + x₂ ，解得

A = ，φ= arctg

显然，当φ₂－φ₁ = 2kπ时（k = 0，±1，±2，…），合振幅A最大，当φ₂－φ₁ = （2k + 1）π时（k = 0，±1，±2，…），合振幅最小。

b、方向垂直、同频率振动合成。当质点同时参与两个垂直的振动x = A₁cos(ωt + φ₁)和y = A₂cos(ωt + φ₂)时，这两个振动方程事实上已经构成了质点在二维空间运动的轨迹参数方程，消去参数t后，得一般形式的轨迹方程为

+－2cos(φ₂－φ₁) = sin²(φ₂－φ₁)

显然，当φ₂－φ₁ = 2kπ时（k = 0，±1，±2，…），有y = x ，轨迹为直线，合运动仍为简谐运动；

当φ₂－φ₁ = （2k + 1）π时（k = 0，±1，±2，…），有+= 1 ，轨迹为椭圆，合运动不再是简谐运动；

当φ₂－φ₁取其它值，轨迹将更为复杂，称“李萨如图形”，不是简谐运动。

c、同方向、同振幅、频率相近的振动合成。令x₁ = Acos(ω₁t + φ)和x₂ = Acos(ω₂t + φ) ，由于合运动x = x₁ + x₂ ，得：x =（2Acost）cos（t +φ）。合运动是振动，但不是简谐运动，称为角频率为的“拍”现象。

4、简谐运动的周期

由②式得：ω= ，而圆周运动的角速度和简谐运动的角频率是一致的，所以

T = 2π ⑤

5、简谐运动的能量

一个做简谐运动的振子的能量由动能和势能构成，即

= mv² + kx² = kA²

注意：振子的势能是由（回复力系数）k和（相对平衡位置位移）x决定的一个抽象的概念，而不是具体地指重力势能或弹性势能。当我们计量了振子的抽象势能后，其它的具体势能不能再做重复计量。

6、阻尼振动、受迫振动和共振

和高考要求基本相同。

二、机械波

1、波的产生和传播

产生的过程和条件；传播的性质，相关参量（决定参量的物理因素）

2、机械波的描述

a、波动图象。和振动图象的联系

b、波动方程

如果一列简谐波沿x方向传播，振源的振动方程为y = Acos（ωt + φ），波的传播速度为v ，那么在离振源x处一个振动质点的振动方程便是

y = Acos〔ωt + φ - ·2π〕= Acos〔ω（t - ）+ φ〕

这个方程展示的是一个复变函数。对任意一个时刻t ，都有一个y（x）的正弦函数，在x-y坐标下可以描绘出一个瞬时波形。所以，称y = Acos〔ω（t - ）+ φ〕为波动方程。

3、波的干涉

a、波的叠加。几列波在同一介质种传播时，能独立的维持它们的各自形态传播，在相遇的区域则遵从矢量叠加（包括位移、速度和加速度的叠加）。

b、波的干涉。两列波频率相同、相位差恒定时，在同一介质中的叠加将形成一种特殊形态：振动加强的区域和振动削弱的区域稳定分布且彼此隔开。

我们可以用波程差的方法来讨论干涉的定量规律。如图2所示，我们用S₁和S₂表示两个波源，P表示空间任意一点。

当振源的振动方向相同时，令振源S₁的振动方程为y₁ = A₁cosωt ，振源S₁的振动方程为y₂ = A₂cosωt ，则在空间P点（距S₁为r₁ ，距S₂为r₂），两振源引起的分振动分别是

y₁′= A₁cos〔ω（t ? ）〕

y₂′= A₂cos〔ω（t ? ）〕

P点便出现两个频率相同、初相不同的振动叠加问题（φ₁ = ，φ₂ = ），且初相差Δφ= （r₂ – r₁）。根据前面已经做过的讨论，有

r₂ ? r₁ = kλ时（k = 0，±1，±2，…），P点振动加强，振幅为A₁ + A₂ ；

r₂ ? r₁ =（2k ? 1）时（k = 0，±1，±2，…），P点振动削弱，振幅为│A₁－A₂│。

4、波的反射、折射和衍射

知识点和高考要求相同。

5、多普勒效应

当波源或者接受者相对与波的传播介质运动时，接收者会发现波的频率发生变化。多普勒效应的定量讨论可以分为以下三种情况（在讨论中注意：波源的发波频率f和波相对介质的传播速度v是恒定不变的）——

a、只有接收者相对介质运动（如图3所示）

设接收者以速度v₁正对静止的波源运动。

如果接收者静止在A点，他单位时间接收的波的个数为f ，

当他迎着波源运动时，设其在单位时间到达B点，则= v₁ ，、

在从A运动到B的过程中，接收者事实上“提前”多接收到了n个波

n = = =

显然，在单位时间内，接收者接收到的总的波的数目为：f + n = f ，这就是接收者发现的频率f₁。即

f₁= f

显然，如果v₁背离波源运动，只要将上式中的v₁代入负值即可。如果v₁的方向不是正对S ，只要将v₁出正对的分量即可。

b、只有波源相对介质运动（如图4所示）

设波源以速度v₂正对静止的接收者运动。

如果波源S不动，在单位时间内，接收者在A点应接收f个波，故S到A的距离：= fλ

在单位时间内，S运动至S′，即= v₂ 。由于波源的运动，事实造成了S到A的f个波被压缩在了S′到A的空间里，波长将变短，新的波长

λ′= = = =

而每个波在介质中的传播速度仍为v ，故“被压缩”的波（A接收到的波）的频率变为

f₂ = = f

当v₂背离接收者，或有一定夹角的讨论，类似a情形。

c、当接收者和波源均相对传播介质运动

当接收者正对波源以速度v₁（相对介质速度）运动，波源也正对接收者以速度v₂（相对介质速度）运动，我们的讨论可以在b情形的过程上延续…

f₃ = f₂ = f

关于速度方向改变的问题，讨论类似a情形。

6、声波

a、乐音和噪音

b、声音的三要素：音调、响度和音品

c、声音的共鸣

第二讲重要模型与专题

一、简谐运动的证明与周期计算

物理情形：如图5所示，将一粗细均匀、两边开口的U型管固定，其中装有一定量的水银，汞柱总长为L 。当水银受到一个初始的扰动后，开始在管中振动。忽略管壁对汞的阻力，试证明汞柱做简谐运动，并求其周期。

模型分析：对简谐运动的证明，只要以汞柱为对象，看它的回复力与位移关系是否满足定义式①，值得注意的是，回复力系指振动方向上的合力（而非整体合力）。当简谐运动被证明后，回复力系数k就有了，求周期就是顺理成章的事。

本题中，可设汞柱两端偏离平衡位置的瞬时位移为x 、水银密度为ρ、U型管横截面积为S ，则次瞬时的回复力

ΣF = ρg2xS = x

由于L、m为固定值，可令： = k ，而且ΣF与x的方向相反，故汞柱做简谐运动。

周期T = 2π= 2π

答：汞柱的周期为2π 。

学生活动：如图6所示，两个相同的柱形滚轮平行、登高、水平放置，绕各自的轴线等角速、反方向地转动，在滚轮上覆盖一块均质的木板。已知两滚轮轴线的距离为L 、滚轮与木板之间的动摩擦因素为μ、木板的质量为m ，且木板放置时，重心不在两滚轮的正中央。试证明木板做简谐运动，并求木板运动的周期。

思路提示：找平衡位置（木板重心在两滚轮中央处）→ú力矩平衡和Σ?F₆= 0结合求两处弹力→ú求摩擦力合力…

答案：木板运动周期为2π 。

巩固应用：如图7所示，三根长度均为L = 2.00m地质量均匀直杆，构成一正三角形框架ABC，C点悬挂在一光滑水平轴上，整个框架可绕转轴转动。杆AB是一导轨，一电动松鼠可在导轨上运动。现观察到松鼠正在导轨上运动，而框架却静止不动，试讨论松鼠的运动是一种什么样的运动。

解说：由于框架静止不动，松鼠在竖直方向必平衡，即：松鼠所受框架支持力等于松鼠重力。设松鼠的质量为m ，即：

N = mg ①

再回到框架，其静止平衡必满足框架所受合力矩为零。以C点为转轴，形成力矩的只有松鼠的压力N、和松鼠可能加速的静摩擦力f ，它们合力矩为零，即：

M_N = M_f

现考查松鼠在框架上的某个一般位置（如图7，设它在导轨方向上距C点为x），上式即成：

N·x = f·Lsin60° ②

解①②两式可得：f = x ，且f的方向水平向左。

根据牛顿第三定律，这个力就是松鼠在导轨方向上的合力。如果我们以C在导轨上的投影点为参考点，x就是松鼠的瞬时位移。再考虑到合力与位移的方向因素，松鼠的合力与位移满足关系——

= －k

其中k = ，对于这个系统而言，k是固定不变的。

显然这就是简谐运动的定义式。

答案：松鼠做简谐运动。

评说：这是第十三届物理奥赛预赛试题，问法比较模糊。如果理解为定性求解，以上答案已经足够。但考虑到原题中还是有定量的条件，所以做进一步的定量运算也是有必要的。譬如，我们可以求出松鼠的运动周期为：T = 2π = 2π = 2.64s 。

二、典型的简谐运动

1、弹簧振子

物理情形：如图8所示，用弹性系数为k的轻质弹簧连着一个质量为m的小球，置于倾角为θ

测试点距岸距离 x/m	0	1	2	3	4	5	6
管内外高度差　 h/cm	0	0.8	3.2	7.2	12.8	20.0	28.8
相应的水流速度 v/ms^-1	______	______	______	______	______	______	______

试题分类