题目内容
如图所示，光滑管形圆轨道半径为R（管径远小于R），固定在竖直面内，小球质量为m，其直径略小于管径，能在管中无摩擦运动，若小球通过轨道最低点时速度为v，以下说法正确的是（ ）
A．速度v至少为
，小球才能在管内做完整的圆周运动B．当
时，小球在轨道最高点对轨道无压力C．小球做完整的圆周运动时，在最低点和最高点的向心力之差为5mg
D．只要
，小球在轨道最低点和最高点的压力之差为6mg
【答案】分析：小球在竖直光滑轨道内运动时，机械能守恒，在最高点与最低点分别列向心力公式飞，然后联立机械能守恒方程即可求解．注意本题中只要小球在最高点的速度大于零，即可完成圆周运动．
解答：解：只要最高点速度大于零即可完成圆周运动，设最高点速度为v1，由机械能守恒得：
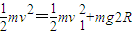，能完成圆周运动的条件为v1≥0，即
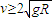，故A错误；
当在最高点满足：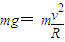
，即
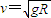时，小球在轨道最高点对轨道无压力，h与R关心不知，故B错误；
当在最高点速度小于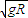
时，轨道给小球向上的支持力此时有：
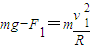①
在最低点有：
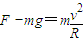②
从最低点到最高点机械能守恒有：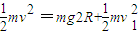
③
联立①②③得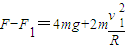
，故C错误；
当在最高点速度大于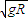
，即最低速度大于
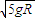时，最高点小球受到轨道给其向下的支持力，此时有：
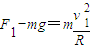④
联立②③④得：F-F1=6mg，故D正确．
故选D．
点评：解决小球在竖直平面内的圆周运动，一般需要根据功能关系和向心力公式分别列方程求解．
解答：解：只要最高点速度大于零即可完成圆周运动，设最高点速度为v1，由机械能守恒得：
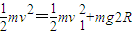，能完成圆周运动的条件为v1≥0，即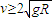，故A错误；当在最高点满足：
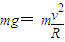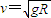，即时，小球在轨道最高点对轨道无压力，h与R关心不知，故B错误；当在最高点速度小于
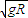时，轨道给小球向上的支持力此时有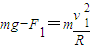： ①在最低点有：
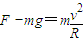②从最低点到最高点机械能守恒有：
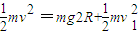③联立①②③得
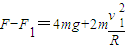，故C错误；当在最高点速度大于
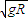，即最低速度大于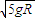时，最高点小球受到轨道给其向下的支持力，此时有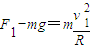： ④联立②③④得：F-F1=6mg，故D正确．
故选D．
点评：解决小球在竖直平面内的圆周运动，一般需要根据功能关系和向心力公式分别列方程求解．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
如图所示，光滑圆管形轨道AB部分平直，BC部分是处于竖直平面内半径为R的半圆，圆管截面半径r＜＜R．有一质量为m、半径比r略小的光滑小球以水平初速度v0射入圆管，问：
（1）如图所示，某种变速自行车有三个链轮和六个飞轮，链轮和飞轮的齿数如下表所示．该自行车的前后轮周长为2m，人脚踩踏板的转速为每秒钟1.5转．若采用的链轮和飞轮齿数分别为48和24，则该种组合下自行车行驶时的速度为
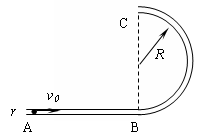
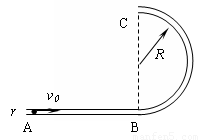
如图所示，光滑圆管形轨道AB部分平直，BC部分是处于竖直平面内半径为R的半圆，圆管截面半径r＜＜R．有一质量为m、半径比r略小的光滑小球以水平初速度v0射入圆管，问：