题目内容
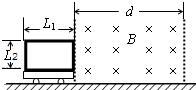 如图所示,水平面上有一个动力小车,在动力小车上竖直固定着一个长度L1、宽度L2的矩形线圈,线圈匝线为n,总电阻为R,小车和线圈的总质量为m,小车运动过程所受摩擦力为f.小车最初静止,线圈的右边刚好与宽为d(d>L1)的有界磁场的左边界重合.磁场方向与线圈平面垂直,磁感应强度为B.现控制动力小车牵引力的功率,让它以恒定加速度a进入磁场,线圈全部进入磁场后,开始做匀速直线运动,直至完全离开磁场,整个过程中,牵引力的总功为W.
如图所示,水平面上有一个动力小车,在动力小车上竖直固定着一个长度L1、宽度L2的矩形线圈,线圈匝线为n,总电阻为R,小车和线圈的总质量为m,小车运动过程所受摩擦力为f.小车最初静止,线圈的右边刚好与宽为d(d>L1)的有界磁场的左边界重合.磁场方向与线圈平面垂直,磁感应强度为B.现控制动力小车牵引力的功率,让它以恒定加速度a进入磁场,线圈全部进入磁场后,开始做匀速直线运动,直至完全离开磁场,整个过程中,牵引力的总功为W.(1)求线圈进入磁场过程中,感应电流的最大值和通过导线横截面的电量.
(2)求线圈进入磁场过程中,线圈中产生的焦耳热.
(3)写出整个过程中,牵引力的功率随时间变化的关系式.
分析:(1)由题,线框先做匀加速运动后匀速运动,当线框刚进入磁场时,速度最大,感应电流也最大,根据运动学公式求出此时的速度,由E=BLv和欧姆定律求解最大感应电流.由法拉第电磁感应定律、欧姆定律等推导出通过导线横截面的电量.
(2)根据功能关系得知,整个过程中,牵引力的总功W等于回路中产生的焦耳热、摩擦生热和线框的动能,由焦耳定律求出线框穿出磁场时焦耳热,即可求出线圈进入磁场过程中产生的焦耳热.
(3)根据牛顿第二定律分三段求解牵引力的功率随时间变化的关系式:线框进入磁场、完全在磁场中、穿出磁场.
(2)根据功能关系得知,整个过程中,牵引力的总功W等于回路中产生的焦耳热、摩擦生热和线框的动能,由焦耳定律求出线框穿出磁场时焦耳热,即可求出线圈进入磁场过程中产生的焦耳热.
(3)根据牛顿第二定律分三段求解牵引力的功率随时间变化的关系式:线框进入磁场、完全在磁场中、穿出磁场.
解答:解:(1)全部进入磁场时速度:v=
最大电动势:Em=nBL2v
最大电流为:Im=
=
q=
△t=
?△t=n
?
=n
=
(2)设进入和离开磁场过程中,线圈产生的焦耳热分别为Q入和Q出,则在整个过程中,
牵引力的总功:W=Q入+Q出+f(L1+d)+
mv2
Q出=
Rt出,
t出=
;
将Im及v代入
得:Q出=
解得:Q入=W-f(L1+d)-maL1-
(3)①小车进入磁场阶段做匀加速运动:
0<t<
,vt=at,I=
由
-f-nBIL2=ma得:P=
t2+(f+ma)at,(0<t<
)
②小车完全在磁场中运动:P=f
,(
<t<(
+
))
③小车匀速穿出磁场的过程:P=(F安+f)v
得P=
+f
((
+
)<t<(
+
))
答:
(1)线圈进入磁场过程中,感应电流的最大值是
,通过导线横截面的电量
.
(2)线圈进入磁场过程中,线圈中产生的焦耳热是W-f(L1+d)-maL1-
.
(3)在整个过程中,牵引力的功率随时间变化的关系式是)①小车进入磁场阶段做匀加速运动:
P=
t2+(f+ma)at,(0<t<
)
②小车完全在磁场中运动:P=f
,(
<t<(
+
))
③小车匀速穿出磁场的过程:P=
+f
((
+
)<t<(
+
)).
| 2aL1 |
最大电动势:Em=nBL2v

最大电流为:Im=
| Em |
| R |
nBL2
| ||
| R |
q=
. |
| I |
| ||
| R |
| △? |
| △t |
| △t |
| R |
| △? |
| R |
| nBL1L2 |
| R |
(2)设进入和离开磁场过程中,线圈产生的焦耳热分别为Q入和Q出,则在整个过程中,
牵引力的总功:W=Q入+Q出+f(L1+d)+
| 1 |
| 2 |
Q出=
| I | 2 m |
t出=
| L1 |
| v |
将Im及v代入
得:Q出=
n2B2
| ||||
| R |
解得:Q入=W-f(L1+d)-maL1-
n2B2
| ||||
| R |
(3)①小车进入磁场阶段做匀加速运动:
0<t<
|
| nBL2vt |
| R |
由
| P |
| vt |
| n2B2L22a2 |
| R |
|
②小车完全在磁场中运动:P=f
| 2aL1 |
|
|
| d-L1 | ||
|
③小车匀速穿出磁场的过程:P=(F安+f)v
得P=
| 2an2B2L1L22 |
| R |
| 2aL1 |
|
| d-L1 | ||
|
|
| d | ||
|
答:
(1)线圈进入磁场过程中,感应电流的最大值是
nBL2
| ||
| R |
| nBL1L2 |
| R |
(2)线圈进入磁场过程中,线圈中产生的焦耳热是W-f(L1+d)-maL1-
n2B2
| ||||
| R |
(3)在整个过程中,牵引力的功率随时间变化的关系式是)①小车进入磁场阶段做匀加速运动:
P=
| n2B2L22a2 |
| R |
|
②小车完全在磁场中运动:P=f
| 2aL1 |
|
|
| d-L1 | ||
|
③小车匀速穿出磁场的过程:P=
| 2an2B2L1L22 |
| R |
| 2aL1 |
|
| d-L1 | ||
|
|
| d | ||
|
点评:本题是电磁感应与力学知识的综合,安培力是关键量.运用功能关系,要分析回路中涉及几种形式的能,能量如何转化.

练习册系列答案
相关题目
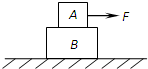 如图所示,水平面上有A、B两物体叠放在一起,现有一水平恒力F作用在A物体上,恰能使A、B两物体一起沿水平面做匀速运动.在运动过程中突然将作用在A上的恒力F撤去迅速作用在B上,并保持大小、方向不变,则A、B的运动状态为( )
如图所示,水平面上有A、B两物体叠放在一起,现有一水平恒力F作用在A物体上,恰能使A、B两物体一起沿水平面做匀速运动.在运动过程中突然将作用在A上的恒力F撤去迅速作用在B上,并保持大小、方向不变,则A、B的运动状态为( )| A、一起匀速直线运动 | B、一起加速运动 | C、B加速、A减速 | D、无法判断,因为A、B的质量关系及接触面间的摩擦情况未知 |
 如图所示,水平面上有一重为40N的物体,受到F1=13N和F2=6N的水平力的作用而保持静止,F1与F2的方向相反.物体与水平面间的动摩擦因数μ=0.2,设最大的静摩擦力等于滑动摩擦力.求:
如图所示,水平面上有一重为40N的物体,受到F1=13N和F2=6N的水平力的作用而保持静止,F1与F2的方向相反.物体与水平面间的动摩擦因数μ=0.2,设最大的静摩擦力等于滑动摩擦力.求: 如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R=3.0Ω的定值电阻,导体棒ab长L=0.5m,其电阻为r=1.0Ω,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.求:
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R=3.0Ω的定值电阻,导体棒ab长L=0.5m,其电阻为r=1.0Ω,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.求: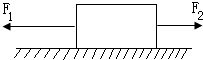 如图所示,水平面上有一重40N的物体,受到F1=12N和F2=6N的水平力作用而保持静止.已知物体与水平面间的动摩擦因数为μ=0.2,求:
如图所示,水平面上有一重40N的物体,受到F1=12N和F2=6N的水平力作用而保持静止.已知物体与水平面间的动摩擦因数为μ=0.2,求: