Question

【题目】某人在静水中游泳，速度为千米/时，现在他在水流速度为4千米/时的河中游泳.

（1）若他沿垂直于岸边的方向游向河对岸，则他实际沿什么方向前进？实际前进的速度大小为多少？

（2）他必须朝哪个方向游，才能沿与水流垂直的方向前进？实际前进的速度大小为多少？

Answer 1

【答案】（1）沿与河岸成60°的夹角顺着水流的方向前进，速度大小为8千米/时 （2）沿向量的方向逆着水流且与河岸所成夹角的余弦值为游，实际前进的速度大小为千米/时

【解析】

作出示意图，再根据向量加法与减法的三角形法则和锐角三角函数的定义即可得出答案．

解：（1）如图，设此人游泳的速度为，水流的速度为，

以OA，OB为邻边作QACB，则此人的实际速度为，

由勾股定理知，且在中，∠COA=60°，

故此人沿与河岸成60°的夹角顺着水流的方向前进，速度大小为8千米/时；

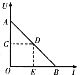
（2）如图，设此人的实际速度为，水流速度为，则游速为，

在Rt△AOD中，，，则，，

故此人沿向量的方向逆着水流且与河岸所成夹角的余弦值为游，实际前进的速度大小为千米/时．