题目内容
6. 如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力Ffmax=8.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑,忽略小滑轮的影响),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,求木块到O点的距离的范围(取g=10m/s2,M、m均视为质点).
如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力Ffmax=8.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑,忽略小滑轮的影响),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,求木块到O点的距离的范围(取g=10m/s2,M、m均视为质点).
分析 当M所受的最大静摩擦力沿半径方向向外时,半径最小,当M所受的最大静摩擦力沿半径向内时,半径最大,根据牛顿第二定律求出木块到O点的距离的范围.
解答 解:当M有远离轴心运动的趋势时,有:
mg+Ffmax=Mω2rmax
当M有靠近轴心运动的趋势时,有:
mg-Ffmax=Mω2rmin
解得:rmax=0.36 m,rmin=0.04 m
即0.04m≤r≤0.36 m.
答:木块到O点的距离的范围为0.04m≤r≤0.36 m.
点评 解决本题的关键搞清圆周运动向心力的来源,抓住临界状态,运用牛顿第二定律进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列说法正确的是( )
| A. | 物体加速下降,重力做正功 | |
| B. | 物体减速下降,重力做正功 | |
| C. | 摩擦力 f1 做正功,它的反作用力 f2 一定做负功 | |
| D. | 摩擦力 f1 做正功,它的反作用力 f2 可能不做功 |
14.如图甲所示,甲为一台小型发电机构造示意图,线圈逆时针转动,产生的电动势随时间变化的正弦规律如图乙所示.发电机线圈内阻为1Ω,外接灯泡的电阻为9Ω恒定不变,则下列说法中正确的为( ) 

| A. | 电压表的示数为6V | |
| B. | 通过电阻的电流方向1秒钟改变50次 | |
| C. | 在0.01s时刻,穿过线圈的磁通量最大 | |
| D. | 产生该交变电流的线圈在磁场中匀速转动的角速度为50π rad/s |
11.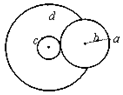 如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
 如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )| A. | b点与d点的线速度大小相等 | |
| B. | a点与c点的线速度大小相等 | |
| C. | c点与b点的角速度大小不相等 | |
| D. | a点与d点的向心加速度大小之比为1:8 |
18.关于匀速圆周运动中的向心加速度说法不正确的是( )
| A. | 向心加速度方向不变,总是指向圆心 | |
| B. | 向心加速度大小保持不变 | |
| C. | 向心加速度可以用线速度和半径表示 | |
| D. | 是表征线速度方向变化快慢的物理量 |
15. 当转台匀速转动时,用同种材料制成的a、b、c三个物体都相对于转台静止不动,如图所示.若ma=2mb=2mc,rc=2ra=2rb,则下列说法中正确的是( )
当转台匀速转动时,用同种材料制成的a、b、c三个物体都相对于转台静止不动,如图所示.若ma=2mb=2mc,rc=2ra=2rb,则下列说法中正确的是( )
 当转台匀速转动时,用同种材料制成的a、b、c三个物体都相对于转台静止不动,如图所示.若ma=2mb=2mc,rc=2ra=2rb,则下列说法中正确的是( )
当转台匀速转动时,用同种材料制成的a、b、c三个物体都相对于转台静止不动,如图所示.若ma=2mb=2mc,rc=2ra=2rb,则下列说法中正确的是( )| A. | 物体a所受的静摩擦力大于c所受的静摩擦力 | |
| B. | 物体b所受的静摩擦力最小 | |
| C. | 物体c的向心加速度最小 | |
| D. | 转速缓慢增大时,物体a最先开始滑动 |
16.下列说法正确的是( )
| A. | 一群处于n=5 的激发态的氢原子向低能级跃迁时最多能辐射出10 种不同频率的光 | |
| B. | 在光电效应实验中,用同种频率的光照射不同的金属表面,从金属表面逸出的光电子的最大初动能Ek 越大,则这种金属的逸出功W0 越大 | |
| C. | 氡元素的半衰期为3.8 天,若有8个氡原子核,则7.6 天后还剩2 个氡原子核未衰变 | |
| D. | 某放射性原子核经过2 次α 衰变和一次β 衰变,核内中子数减少了5 个 |