题目内容
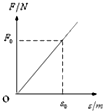
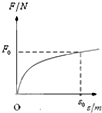
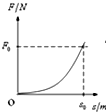
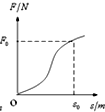
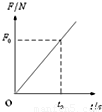
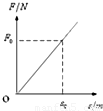
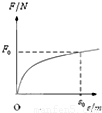
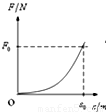
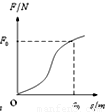
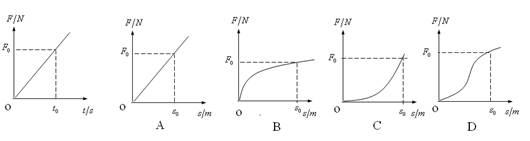
 水平光滑的地面上有一质量为m的木块,从某时刻计时t=0,对物体施加一水平外力,方向不变,大小随时间成正比,即F=kt,物体在外力作用下沿力方向作加速运动.在t=t0时刻,物体的位移s=s0,则在此过程中,力随位移的变化关系图象大致是( )
水平光滑的地面上有一质量为m的木块,从某时刻计时t=0,对物体施加一水平外力,方向不变,大小随时间成正比,即F=kt,物体在外力作用下沿力方向作加速运动.在t=t0时刻,物体的位移s=s0,则在此过程中,力随位移的变化关系图象大致是( )分析:根据动量定理并利用微元法列式求解出速度的瞬时表达式;再利用微元法求解出位移与时间关系表达式;最后得带力F与位移关系表达式进行讨论.
解答:解:根据题意,有:F=kt;
根据动量定理,有:∑F?△t=m?∑△v;
联立解得:v=
kmt2∝t2
位移S=∑v?△t=
kmt3,故位移与时间的三次方成正比;
故:S=
Fmt2,F-t图象是抛物线,故ACD错误,B正确;
故选B.
根据动量定理,有:∑F?△t=m?∑△v;
联立解得:v=
| 1 |
| 2 |
位移S=∑v?△t=
| 1 |
| 6 |
故:S=
| 1 |
| 6 |
故选B.
点评:本题关键是根据动量定理列式求解速度,两次用到微元法,要熟悉微积分,较难.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目

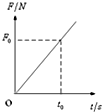 水平光滑的地面上有一质量为m的木块,从某时刻计时t=0,对物体施加一水平外力,方向不变,大小随时间成正比,即F=kt,物体在外力作用下沿力方向作加速运动.在t=t0时刻,物体的位移s=s0,则在此过程中,力随位移的变化关系图象大致是
水平光滑的地面上有一质量为m的木块,从某时刻计时t=0,对物体施加一水平外力,方向不变,大小随时间成正比,即F=kt,物体在外力作用下沿力方向作加速运动.在t=t0时刻,物体的位移s=s0,则在此过程中,力随位移的变化关系图象大致是