题目内容
如图所示,位于同一水平面内的、两根平行的光滑金属导轨,处在匀强磁场中,磁场方向垂直于导轨所在平面,导轨的一端与一电阻相连;具有一定质量的金属杆ab放在导轨上并与导轨垂直。现用一平行于导轨的恒力F拉杆ab,使它由静止开始向右运动。杆和导轨的电阻、感应电流产生的磁场均可不计。用E表示回路中的感应电动势;i表示回路中的感应电流,在i随时间增大的过程中,电阻消耗的功率等于( )
A.F的功率 B.安培力的功率的绝对值
C.F与安培力的合力的功率 D.iE
BD
解析:杆切割磁感线产生感应电动势与导轨、电阻R组成闭合电路,从而杆受安培力作用,还受恒力F。由牛顿第二定律得:F-Fa=ma又Fa=BIl=![]() ,故杆先做a↓的变加速运动。在此过程中,恒力F做的功转化为电能和杆的动能。电能再转化为电阻R的焦耳热。故A错,C错、克服安培力做功将其他形式能转化为电能。B正确。由闭合电路知识知D正确。
,故杆先做a↓的变加速运动。在此过程中,恒力F做的功转化为电能和杆的动能。电能再转化为电阻R的焦耳热。故A错,C错、克服安培力做功将其他形式能转化为电能。B正确。由闭合电路知识知D正确。

练习册系列答案
相关题目
 如图所示,同一物块分别放在水平面和固定斜面上,在两个大小相等的推力F1、F2作用下运动,F1、F2方向分别平行于水平面和斜面.若物块在推力作用下通过的位移大小相等,则推力F1、F2对物块所做的功( )
如图所示,同一物块分别放在水平面和固定斜面上,在两个大小相等的推力F1、F2作用下运动,F1、F2方向分别平行于水平面和斜面.若物块在推力作用下通过的位移大小相等,则推力F1、F2对物块所做的功( )| A、相等 | B、与物块和接触面的粗糙程度有关 | C、在水平面上推力所做的功较多 | D、在斜面上推力所做的功较多 |

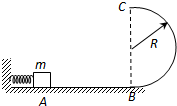 如图所示,光滑水平面AB与位于竖直面内的半圆形轨道在B点平滑连接,半圆形轨道表面粗糙,半径为R.一个质量为m的静止小物块在A点处压紧弹簧,弹簧弹开时小物块在弹力的作用下获得动能向右运动,当它到达B点进入半圆轨道的瞬间,小物块对轨道的压力为其自身重力的7倍,之后沿轨道向上恰能完成圆运动到达C点.求:
如图所示,光滑水平面AB与位于竖直面内的半圆形轨道在B点平滑连接,半圆形轨道表面粗糙,半径为R.一个质量为m的静止小物块在A点处压紧弹簧,弹簧弹开时小物块在弹力的作用下获得动能向右运动,当它到达B点进入半圆轨道的瞬间,小物块对轨道的压力为其自身重力的7倍,之后沿轨道向上恰能完成圆运动到达C点.求: