题目内容
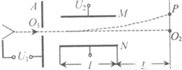
如图所示是示波器的原理示意图.电子从灯丝发射出来,经电压为U1的电场加速后,通过加速极板A上的小孔O1射出,然后沿中心线O1O2进入M、N间的偏转电场,偏转电场的电压为U2,场强方向垂直于O1O2,电子离开偏转电场后,最终打在垂直于O1O2放置的荧光屏上的P点.已知电子的电荷量为e,平行金属板M、N间的距离为d,极板长为l,极板右端与荧光屏之间的距离为L,电子离开灯丝时的初速度可忽略,电子所受重力以及电子之间的相互作用力不计.(1)若把P点到O2点的距离称为偏转距离Y,其偏转距离Y为多少?
(2)求电子即将到达P点时的动能.
【答案】分析:(1)根据动能定理求出电子射入偏转电场时的速度,电子进入偏转电场后做类平抛运动,根据动力学知识求出离开偏转电场时的偏转位移,离开偏转电场时速度的反向延长线经过偏转电场中轴线的中点,根据这一推论,利用比例式求出偏转距离Y.
(2)电子从静止开始运动打到P点的过程中,有加速电场做功和偏转电场做功,根据动能定理求出打在P点的动能.
解答:解:(1)设电子到达O1时的速度为v,则
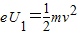
设电子在偏转电场MN中运动的加速度为a,运动时间为t,则
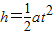
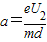
t=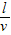
解得: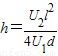
由: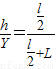
解得: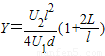
故偏转距离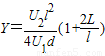 .
.
(2)由动能定理:eU1+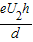 =EKP-0
=EKP-0
得:EKP=eU1+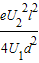
故电子即将到达P点时的动能为eU1+ .
.
点评:解决本题的关键知道电子的运动规律,现在加速电场中加速,然后进入偏转电场做类平抛运动,离开偏转电场做匀速直线运动.
(2)电子从静止开始运动打到P点的过程中,有加速电场做功和偏转电场做功,根据动能定理求出打在P点的动能.
解答:解:(1)设电子到达O1时的速度为v,则
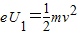
设电子在偏转电场MN中运动的加速度为a,运动时间为t,则
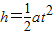
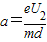
t=
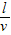
解得:
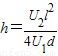
由:
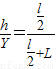
解得:
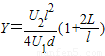
故偏转距离
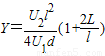 .
.(2)由动能定理:eU1+
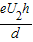 =EKP-0
=EKP-0得:EKP=eU1+
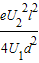
故电子即将到达P点时的动能为eU1+
 .
.点评:解决本题的关键知道电子的运动规律,现在加速电场中加速,然后进入偏转电场做类平抛运动,离开偏转电场做匀速直线运动.

练习册系列答案
相关题目
 一个探究性学习小组利用示波器,绘制出了一个原、副线圈匝数比为2:1的理想变压器,副线圈两端输出电压u随时间t变化的图象如图所示(图线为正弦曲线).则下列说法错误的是( )
一个探究性学习小组利用示波器,绘制出了一个原、副线圈匝数比为2:1的理想变压器,副线圈两端输出电压u随时间t变化的图象如图所示(图线为正弦曲线).则下列说法错误的是( )| A、该变压器原线圈输入电压的瞬时值表达式为u=20sin(100πt)V | B、接在副线圈两端的交流电压表的示数为7.1V | C、该变压器原线圈输入频率为50 Hz | D、接在副线圈两端阻值为20Ω的白炽灯,消耗的功率为2.5W |
一个探究性学习小组利用示波器,绘制出了一个
原、副线圈匝数比为2∶1的理想变压器,副线圈两
端输出电压u随时间t变化的图象如图所示
(图线为正弦曲线)。
则下列说法错误的是
A.该变压器原线圈输入电压的瞬时值表达式为u=20sin(100 t)V t)V |
| B.接在副线圈两端的交流电压表的示数为7.1V |
| C.该变压器原线圈输入频率为50 Hz |
| D.接在副线圈两端阻值为20 Ω的白炽灯,消耗的功率为2.5W |

 t)V
t)V




