题目内容
在水平直轨道上有两辆长为l的汽车,中心相距为s,开始时,A车在后面以初速v0、加速度大小为2a正对着B车做匀减速直线运动,而B车同时以初速为零、加速度大小为a做匀加速直线运动,两车运动方向相同,要使两车不相撞,则v0应满足的关系式为
v0≤
| 6a(s-L) |
v0≤
.| 6a(s-L) |
分析:要使两车不相撞,临界情况是在速度相等时恰好不相撞,根据匀变速直线运动公式求出v0应满足的条件.
解答:解:当两者速度相等时,有v0-2at=at,解得t=
.
此时A车的位移x1=v0t-
?2at2=
B车的位移x2=
at2=
有x1=x2+(s-l)
解得v0=
故v0应满足的关系式为v0≤
.
故答案为:v0≤
.
| v0 |
| 3a |
此时A车的位移x1=v0t-
| 1 |
| 2 |
| 2v02 |
| 9a |
B车的位移x2=
| 1 |
| 2 |
| v02 |
| 18a |
有x1=x2+(s-l)
解得v0=
| 6a(s-L) |
故v0应满足的关系式为v0≤
| 6a(s-L) |
故答案为:v0≤
| 6a(s-L) |
点评:本题是追及问题,在速度相等前,两者的距离越来越小,若未撞上,则速度相等后,两者的距离越来越大,所以只能在速度相等之时或相等之前相撞.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
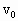 、加速度为a的匀减速直线运动,B同时做初速度为0的匀加速运动,加速度为a/2,两车运动方向相同,要使两车不相撞,
、加速度为a的匀减速直线运动,B同时做初速度为0的匀加速运动,加速度为a/2,两车运动方向相同,要使两车不相撞,