题目内容
AB为斜面，倾角为30°，小球从A点以初速度V水平抛出，恰好落到B点，则A、B间的距离 ，物体在空中飞行的时间 ，到达B点的速度 ．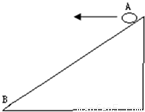
【答案】分析：小球做平抛运动，水平方向做匀速直线运动，竖直方向做自由落体运动，根据几何知识有：tan30°=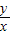
，而水平位移x=LABcos30°=vt，竖直位移y=LABsin30°=
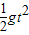，可求出时间，再求解A、B间的距离．由速度的合成求解到达B点的速度．
解答：解：设A、B间距离为L，则有
水平方向：x=Lcos30°=vt，
竖直方向：y=Lsin30°=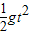
，
又tan30°=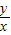
，
联立以上三式得：t=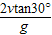
=
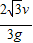
L=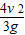
设到达B点的速度为vB=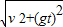
=
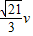
故答案为：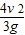
，
，
．
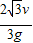点评：本题运用运动的分解和合成法研究平抛运动，关键要抓住斜面的倾角与两个分位移的关系．
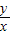，而水平位移x=LABcos30°=vt，竖直位移y=LABsin30°=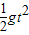，可求出时间，再求解A、B间的距离．由速度的合成求解到达B点的速度．解答：解：设A、B间距离为L，则有
水平方向：x=Lcos30°=vt，
竖直方向：y=Lsin30°=
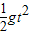，又tan30°=
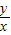，联立以上三式得：t=
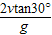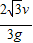
=L=
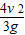
设到达B点的速度为vB=
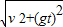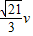
=故答案为：
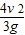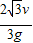，，．点评：本题运用运动的分解和合成法研究平抛运动，关键要抓住斜面的倾角与两个分位移的关系．
练习册系列答案
名校课堂系列答案
相关题目
如图，AB为斜面，倾角为30°，小球从A点以初速度v0水平抛出，恰好落到B点．求：
如图所示，AB为斜面，倾角为α，小球从A点以初速度v0水平抛出，恰好落到B点.求：