题目内容
一个小球在某星球表面做自由落体运动,测得它在时间t内下落h,由此可知该星球表面的重力加速度是
m/s2;小球在通过最后h/3所经历的时间是t的
| 2h |
| t2 |
| 2h |
| t2 |
(1-
)
|
(1-
)
倍.
|
分析:通过自由落体运动的公式h=
gt2求出星球表面重力加速度.
求解自由落体运动中某一段过程时间可以用整个运动时间减去前面过程的运动时间.
| 1 |
| 2 |
求解自由落体运动中某一段过程时间可以用整个运动时间减去前面过程的运动时间.
解答:解:解:(1)根据题意知,石块在星球表面做自由落体运动,
由h=
gt2
解得,g=
小球在通过前
h的时间是t1
h=
g
t1=
t
所以小球在通过最后
所经历的时间是(1-
)t,即是t的(1-
)倍.
故答案为:
,(1-
)
由h=
| 1 |
| 2 |
解得,g=
| 2h |
| t2 |
小球在通过前
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| t | 2 1 |
t1=
|
所以小球在通过最后
| h |
| 3 |
|
|
故答案为:
| 2h |
| t2 |
|
点评:解决本题的关键掌握自由落体运动的位移时间公式.自由落体运动规律在其他星球照样适应.

练习册系列答案
相关题目
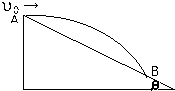 如图,宇航员站在某星球表面上的斜面顶端A处,沿水平方向以初速度V0抛出一个小球.经时间t小球落在斜面上的某一点B处.设空气阻力不计,该星球半径为R,万有引力常数为G.求
如图,宇航员站在某星球表面上的斜面顶端A处,沿水平方向以初速度V0抛出一个小球.经时间t小球落在斜面上的某一点B处.设空气阻力不计,该星球半径为R,万有引力常数为G.求