题目内容
如图所示，P是水平面上的圆弧凹槽．从高台边B点以速度v水平飞出的小球，恰能从固定在某位置的凹槽的圆弧轨道的左端A沿圆弧切线方向进入轨道．O是圆弧的圆心，θ1是OA与竖直方向的夹角，θ2是BA与竖直方向的夹角．则（ ）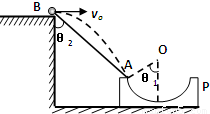
A．cotθ1tanθ2=2
B．tanθ1tanθ2=2
C．cotθ1cotθ2=2
D．tanθ1cotθ2=2
【答案】分析：从图中可以看出，速度与水平方向的夹角为θ1，位移与竖直方向的夹角为θ2．然后求出两个角的正切值．
解答：解：平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动．速度与水平方向的夹角为θ1，
tan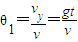
．位移与竖直方向的夹角为θ2，
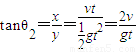，则tanθ1tanθ2=2．故B正确，A、C、D错误．
故选B．
点评：解决本题的关键掌握处理平抛运动的方法，平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动．以及知道速度与水平方向夹角的正切值是同一位置位移与水平方向夹角的正切值的两倍．
解答：解：平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动．速度与水平方向的夹角为θ1，
tan
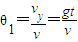．位移与竖直方向的夹角为θ2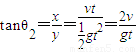，，则tanθ1tanθ2=2．故B正确，A、C、D错误．故选B．
点评：解决本题的关键掌握处理平抛运动的方法，平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动．以及知道速度与水平方向夹角的正切值是同一位置位移与水平方向夹角的正切值的两倍．
练习册系列答案
相关题目
（2008?广东模拟）人们到医院检查身体时，其中有一项就是做胸透，做胸透所用的是X光，…我们可以把做胸透的原理等效如下：如图所示，P是一个放射源，从开口处在纸面内向各个方向放出某种粒子（不计重力），而这些粒子最终必须全部垂直射到底片MN这一有效区域，并要求底片MN上每一地方都有粒子到达．假若放射源所放出的是质量为m、电量为q的带正电的粒子，且所有的粒子速率都是v，M与放射源的出口在同一水平面，底片MN竖直放置，底片MN长为L．为了实现上述目的，我们必须在P的出口处放置一有界匀强磁场．求：
