题目内容
 在建筑装修中,工人用质量为5.0kg 的磨石A对地面和斜壁进行打磨,已知A与地面、A与斜壁之间的动摩擦因数μ均相同.(g 取10/m/s2)
在建筑装修中,工人用质量为5.0kg 的磨石A对地面和斜壁进行打磨,已知A与地面、A与斜壁之间的动摩擦因数μ均相同.(g 取10/m/s2)(1)当A在水平方向的推力F1=25N 作用下打磨地面时,A恰好在水平地面上做匀速直线运动,求A与地面间的动摩擦因数μ.
(2)若用A对倾角θ=37°的斜壁进行打磨(如图所示),当对A施加竖直向上的推力F2为多大时,磨石A能沿斜壁向上做匀速运动.(sin 37°=0.6,cos 37°=0.8)
分析:(1)对物体进行受力分析,根据共点力的平衡可知可求得磨石受到的摩擦力,再根据动摩擦力的公式求得动摩擦因数μ.
(2)对物体进行受力分析,根据平衡条件求出推力F2.
(2)对物体进行受力分析,根据平衡条件求出推力F2.
解答:解:(1)A恰好在水平地面上做匀速直线运动,滑动摩擦力等于推力,即:
f=F1=25.
解得:μ=
=
=
=0.5
(2)先将重力及向上的推力合成后,将二者的合力向垂直于斜面方向及沿斜面方向分解可得:
在沿斜面方向有:(F2-mg)cosθ-f=0;
 在垂直斜面方向上有:FN=(F2-mg)sinθ;
在垂直斜面方向上有:FN=(F2-mg)sinθ;
又 f=μFN=μ(F2-mg)sinθ;
得:(F2-mg)cosθ-μ(F2-mg)sinθ=0
由于μ=0.5,θ=37°,
解得:F2=mg=50N.
答:(1)A与地面间的动摩擦因数μ为0.5.
(2)当对A 施加竖直向上的推力F2 为50N时,磨石A能沿斜壁向上做匀速运动.
f=F1=25.
解得:μ=
| f |
| FN |
| F1 |
| mg |
| 25 |
| 50 |
(2)先将重力及向上的推力合成后,将二者的合力向垂直于斜面方向及沿斜面方向分解可得:
在沿斜面方向有:(F2-mg)cosθ-f=0;
 在垂直斜面方向上有:FN=(F2-mg)sinθ;
在垂直斜面方向上有:FN=(F2-mg)sinθ;又 f=μFN=μ(F2-mg)sinθ;
得:(F2-mg)cosθ-μ(F2-mg)sinθ=0
由于μ=0.5,θ=37°,
解得:F2=mg=50N.
答:(1)A与地面间的动摩擦因数μ为0.5.
(2)当对A 施加竖直向上的推力F2 为50N时,磨石A能沿斜壁向上做匀速运动.
点评:滑动摩擦力的大小一定要注意不但可以由μFN求得,也可以由共点力的平衡或牛顿第二定律求得,故在学习时应灵活掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在建筑装修中,工人用质量为m的磨石对斜壁(斜壁与竖直方向的夹角为θ)进行打磨,如图所示.当对磨石加竖直向上的推力F时,磨石恰好沿斜壁匀速向上运动.已知磨石与斜壁之间的动摩擦因数为μ,则磨石受到的摩擦力是( )
在建筑装修中,工人用质量为m的磨石对斜壁(斜壁与竖直方向的夹角为θ)进行打磨,如图所示.当对磨石加竖直向上的推力F时,磨石恰好沿斜壁匀速向上运动.已知磨石与斜壁之间的动摩擦因数为μ,则磨石受到的摩擦力是( )| A、(mg-F)sinθ | B、μ(mg-F)sinθ | C、μ(F-mg)sinθ | D、(F-mg)cosθ |
 如图所示,在建筑装修中,工人用质量为5.0kg的磨石A对地面和斜壁进行打磨,已知A与地面、A与斜壁之间的动摩擦因数μ均相同.(g取10m/s2 且sin37°=0.6,cos37°=0.8)
如图所示,在建筑装修中,工人用质量为5.0kg的磨石A对地面和斜壁进行打磨,已知A与地面、A与斜壁之间的动摩擦因数μ均相同.(g取10m/s2 且sin37°=0.6,cos37°=0.8) (2012?聊城模拟)在建筑装修中,工人用质量为M的磨石对斜壁进行打磨,当对磨石加竖直向上推力F时,磨石恰好沿斜壁向上匀速运动,已知磨石与斜壁之间的动摩擦因素为μ,则磨石受到的摩擦力是( )
(2012?聊城模拟)在建筑装修中,工人用质量为M的磨石对斜壁进行打磨,当对磨石加竖直向上推力F时,磨石恰好沿斜壁向上匀速运动,已知磨石与斜壁之间的动摩擦因素为μ,则磨石受到的摩擦力是( )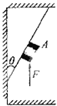 在建筑装修中,工人用质量为m=5.0kg的磨石A对倾角θ=370的斜壁进行打磨,A与斜壁之间的动摩擦因数μ=0.5,如图所示,当对A加竖直向上推力F=60N时,则磨石A从静止开始沿斜壁向上运动2m(斜壁长>2m)所需时间为多少?(g取10m/s2,sin37°=0.6,cos37°=0.8)
在建筑装修中,工人用质量为m=5.0kg的磨石A对倾角θ=370的斜壁进行打磨,A与斜壁之间的动摩擦因数μ=0.5,如图所示,当对A加竖直向上推力F=60N时,则磨石A从静止开始沿斜壁向上运动2m(斜壁长>2m)所需时间为多少?(g取10m/s2,sin37°=0.6,cos37°=0.8)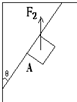 在建筑装修中,工人用质量为5kg的磨石A对地面和斜壁进行打磨,已知磨石A与地面和斜壁之间的动摩擦因数?均相同.
在建筑装修中,工人用质量为5kg的磨石A对地面和斜壁进行打磨,已知磨石A与地面和斜壁之间的动摩擦因数?均相同.