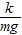Question

如图所示，一个劲度系数为k的轻质弹簧竖直放置在桌面上，弹簧的下端固定于桌面上，上端与质量为M的金属盘固定，金属盘内放一个质量为m的砝码．现让砝码随金属盘一起沿竖直方向做简谐运动．

（1）为了保证砝码不脱离金属盘，振幅最大不能超过多少?

（2）在上述振动过程中，砝码对金属盘的最大压力为多少?

Answer 1

(1)g  (2)2mg

解析：本题主要考查简谐运动的对称性.

(1)分析得砝码在最高点最易脱离.若恰不脱离,砝码只受重力,此时M、m的加速度均为g(向下).

设此时弹簧伸长量为x₁,对M受力分析如图

据牛顿第二定律G+F₁=Ma=Mg

则x₁=0,即弹簧处于原长.

而在平衡位置时,设压缩量为x₂,

对M、m整体受力分析如图

由平衡条件得G′=F₂,(M+m)g=kx₂

x₂=.分析得最大振幅A=x₂=.

(2)由题意分析得,在最低处砝码对金属盘的压力最大，

此时m受力如图.由简谐运动对称性知,此时砝码的加速度亦为g且向上,据牛顿第二定律得

N-G₀=mg  N=2mg  N′=N=2mg.