Question

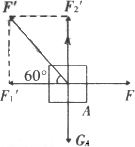
如图所示，物体A重10 N，物体B重10 N，A与水平桌面间的动摩擦因数μ＝0.2，绳重、绳与定滑轮间的摩擦均不计．A处于静止状态，问水平拉力F应取何值？(可认为最大静摩擦力和滑动摩擦力大小相等)

Answer 1

答案：
解析：

隔离出来A为研究对象，画出受力示意图，如图所示．根据题意A静止，应有F合＝0，FN＝G－sin60°，FN＝1.34 N 　　A与桌面间的最大静摩擦力fm＝μFN＝0.27 N，所以静摩擦力的取值范围是0＜Ff≤0.27 N． 　　当F＞时，Ff向左，F的最大值Fmax，由平衡条件 　　Fx＝0，Fmax＝＋fm＝5.27 N． 　　当F＜时，Ff向右，F的最小值Fmin，由平衡条件 　　Fx＝0，Fmin＝－fm＝4.73 N． 　　F的取值范围是4.73 N≤F≤5.27 N．

提示：

思路启迪：隔离物体A，A受的重力、绳的拉力是已知量，桌面给A的支持力FN未知大小，方向向上，A是否受摩擦力Ff属未知量．未知量应由A的平衡状态来定．作出A的受力图，如图所示，再进行估算，判定FN的大小和摩擦力的情况．将正交分解后，FN＝G－sin60°＞0，＝cos60°＝5 N，如果F取5 N满足A静止的条件，由题意A静止，所以Ff＝0，如果F＞5 N．即F＞，Ff向左；如果F＜5 N，即F＜，同理Ff向右．综上分析可知F的取值有一个范围． 　　规律方法：在用正交分解法解题时，坐标系的选择应以尽量少分解力为原则，以简化运算．