题目内容
 如图,质量为M的平板放在倾角为α的固定斜面上,质量为m的滑块放在平板上.两物体通过细线连接,中间夹着一个处于压缩状态的弹簧.当整体一起加速下滑时细线突然断开,已知细线突然断开的瞬间m的加速度为零,一切摩擦不计,斜面足够长.则( )
如图,质量为M的平板放在倾角为α的固定斜面上,质量为m的滑块放在平板上.两物体通过细线连接,中间夹着一个处于压缩状态的弹簧.当整体一起加速下滑时细线突然断开,已知细线突然断开的瞬间m的加速度为零,一切摩擦不计,斜面足够长.则( )分析:通过细线断开瞬间m的瞬时加速度得出弹簧的弹力大小,从而对M分析,根据牛顿第二定律求出M的加速度.当弹簧恢复原长时,根据牛顿第二定律分别求出两物体的加速度,从而进行比较.
解答:解:A、细线断开的瞬间,m的加速度为零,知弹簧的弹力F=mgsinα,隔离对M分析,根据牛顿第二定律得,M的加速度a=
=
.故B正确,A错误.
C、当弹簧恢复原长时,弹簧的弹力相等,m所受的合力为mgsinα,则加速度a=gsinα,对M,所受的合力为Mgsinα,则加速度a′=gsinα,在此过程M向下加速,m向上加速,可知速度不同.故C正确,D错误.
故选BC.
| Mgsinα+F |
| M |
| (M+m)gsinα |
| M |
C、当弹簧恢复原长时,弹簧的弹力相等,m所受的合力为mgsinα,则加速度a=gsinα,对M,所受的合力为Mgsinα,则加速度a′=gsinα,在此过程M向下加速,m向上加速,可知速度不同.故C正确,D错误.
故选BC.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
如图,质量为m的人在质量为M的平板车上从左端走到右端,若不计平板车与地面的摩擦,则下列说法不正确的是
| A.人在车上行走时,车将向左运动 |
| B.当人停止走动时,由于车的惯性大,车将继续后退 |
| C.若人越慢地从车的左端走到右端,则车在地面上移动的距离越大 |
| D.不管人在车上行走的速度多大,车在地面上移动的距离都相同 |
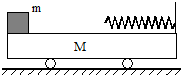 如图,质量为M的平板车静止在光滑的水平地面上,小车的左端放一质量为m的木块,车的右端固定一个轻质弹簧,现给木块一个水平向右的瞬时冲量I,木块便沿车板向右滑行,在与弹簧相碰后又沿原路返回,并且恰好能达到小车的左端.试求:
如图,质量为M的平板车静止在光滑的水平地面上,小车的左端放一质量为m的木块,车的右端固定一个轻质弹簧,现给木块一个水平向右的瞬时冲量I,木块便沿车板向右滑行,在与弹簧相碰后又沿原路返回,并且恰好能达到小车的左端.试求: 如图,质量为m的人在质量为M的平板车上从左端走到右端,若不计平板车与地面的摩擦,则下列说法不正确的是( )
如图,质量为m的人在质量为M的平板车上从左端走到右端,若不计平板车与地面的摩擦,则下列说法不正确的是( ) 如图,质量为m的人在质量为M的平板车上从左端走到右端,若不计平板车与地面的摩擦,则下列说法不正确的是( )
如图,质量为m的人在质量为M的平板车上从左端走到右端,若不计平板车与地面的摩擦,则下列说法不正确的是( )