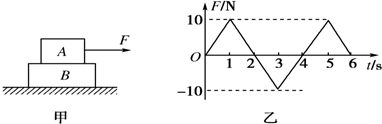题目内容
 如图甲所示,A、B两块金属板水平放置,相距为d=0.6cm,两板间加有一周期性变化的电压,当B板接地(φB=0)时,A板电势φA,随时间变化的情况如图乙所示.现有一带负电的微粒在t=0时刻从B板中央小孔射入电场,若该带电徽粒受到的电场力为重力的两倍,且射入电场时初速度可忽略不计.求:
如图甲所示,A、B两块金属板水平放置,相距为d=0.6cm,两板间加有一周期性变化的电压,当B板接地(φB=0)时,A板电势φA,随时间变化的情况如图乙所示.现有一带负电的微粒在t=0时刻从B板中央小孔射入电场,若该带电徽粒受到的电场力为重力的两倍,且射入电场时初速度可忽略不计.求:(1)在0~
| T |
| 2 |
| T |
| 2 |
(2))要使该微粒不与A板相碰,所加电压的周期最长为多少(g=10m/s2).
分析:(1)根据牛顿第二定律求出加速度的大小和方向.
(2)前半周期粒子向上匀加速运动,后半周期先向上做匀减速运动,后向下加速运动,根据牛顿第二定律和运动学公式求得微粒在一个周期内的总位移,再进行分析计算.
(2)前半周期粒子向上匀加速运动,后半周期先向上做匀减速运动,后向下加速运动,根据牛顿第二定律和运动学公式求得微粒在一个周期内的总位移,再进行分析计算.
解答:解:(1)设电场力大小为F,则F=2mg,对于t=0时刻射入的微粒,在前半个周期内,有
F-mg=ma1
又由题意,F=2mg
解得,a1=g,方向向上.
后半个周期的加速度a2满足
F+mg=ma2
得 a2=3g,方向向下.
(2)前半周期上升的高度h1=
a1(
)2=
gT2
前半周期微粒的末速度为v1=
gT
后半周期先向上做匀减速运动,设减速运动时间t1,则3gt1=
gT,则得t1=
.
此段时间内上升的高度 h2=
a2
=
×3g×(
)2=
则上升的总高度为H=h1+h2=
后半周期的
-t1=
时间内,微粒向下加速运动,下降的高度H3=
×3g×(
)2=
.
上述计算表明,微粒在一个周期内的总位移为零,只要在上升过程中不与A板相碰即可,则H≤d,即
≤d
所加电压的周期最长为Tm=
=6×10-2s
答:
(1)在0~
和
~T这两段时间内微粒的加速度大小和方向分别为:g,方向向上和3g,方向向下;
(2))要使该微粒不与A板相碰,所加电压的周期最长为6×10-2s.
F-mg=ma1
又由题意,F=2mg
解得,a1=g,方向向上.
后半个周期的加速度a2满足
F+mg=ma2
得 a2=3g,方向向下.
(2)前半周期上升的高度h1=
| 1 |
| 2 |
| T |
| 2 |
| 1 |
| 8 |
前半周期微粒的末速度为v1=
| 1 |
| 2 |
后半周期先向上做匀减速运动,设减速运动时间t1,则3gt1=
| 1 |
| 2 |
| T |
| 6 |
此段时间内上升的高度 h2=
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
| T |
| 6 |
| gT2 |
| 24 |
则上升的总高度为H=h1+h2=
| gT2 |
| 6 |
后半周期的
| T |
| 2 |
| T |
| 3 |
| 1 |
| 2 |
| T |
| 3 |
| gT2 |
| 6 |
上述计算表明,微粒在一个周期内的总位移为零,只要在上升过程中不与A板相碰即可,则H≤d,即
| gT2 |
| 6 |
所加电压的周期最长为Tm=
|
答:
(1)在0~
| T |
| 2 |
| T |
| 2 |
(2))要使该微粒不与A板相碰,所加电压的周期最长为6×10-2s.
点评:带电粒子在电场中运动的问题,是电场知识和力学知识的综合应用,分析方法与力学分析方法基本相同,关键在于分析粒子的受力情况和运动情况.

练习册系列答案
相关题目
 如图甲所示,A、B两长方体叠放在一起,放在光滑的水平面上.物体B从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止.则在0~2t0时间内,下列说法正确的是( )
如图甲所示,A、B两长方体叠放在一起,放在光滑的水平面上.物体B从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止.则在0~2t0时间内,下列说法正确的是( )| A、t0时刻,A、B间的静摩擦力最大,加速度最小 | B、t0时刻,A、B的速度最大 | C、0时刻和2t0时刻,A、B间的静摩擦力最大 | D、2t0时刻,A、B离出发点最远,速度为0 |
 如图甲所示,A、B两物体叠放在光滑水平面上,对物体A施加一水平力F,F-t图象如图乙所示,两物体在力F作用下由静止开始运动,且始终相对静止,规定水平向右为正方向,则下列说法正确的是( )
如图甲所示,A、B两物体叠放在光滑水平面上,对物体A施加一水平力F,F-t图象如图乙所示,两物体在力F作用下由静止开始运动,且始终相对静止,规定水平向右为正方向,则下列说法正确的是( ) 如图甲所示,A、B两块金属板水平放置,相距为d=0.6cm,两板间加有一周期性变化的电压,当B板接地(φB=0)时,A板电势φA,随时间变化的情况如图乙所示.现有一带负电的微粒在t=0时刻从B板中央小孔射入电场,若该带电微粒受到的电场力为重力的两倍,且射入电场时初速度可忽略不计.求:(g=10m/s2).
如图甲所示,A、B两块金属板水平放置,相距为d=0.6cm,两板间加有一周期性变化的电压,当B板接地(φB=0)时,A板电势φA,随时间变化的情况如图乙所示.现有一带负电的微粒在t=0时刻从B板中央小孔射入电场,若该带电微粒受到的电场力为重力的两倍,且射入电场时初速度可忽略不计.求:(g=10m/s2).