题目内容
如图所示，在竖直平面内有一个半径为R的圆弧轨道。半径OA水平、OB竖直，一个质量为m的小球自A正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力，已知PA=2R，重力加速度为g，则小球
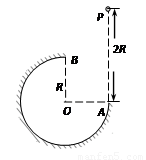
A．从B点飞出后恰能落到A点
B．从P到B的运动过程中机械能守恒
C．从P到B的运动过程中合外力做功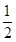
mgR
D．从P到B的运动过程中克服摩擦力做功mgR
【答案】
C
【解析】
试题分析：因为在B点小球恰好对轨道没有压力，所以重力完全充当向心力，即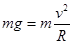
,解得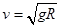
,从B点飞出后，小球做平抛运动，根据
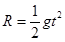可得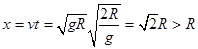
,所以小球飞出A点，A错误，
若机械能守恒，则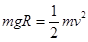
得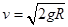
，与上面求出的B点的速度不同，所以机械能不守恒，B错误，
从P到B过程中外力做功为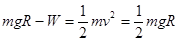
.解得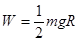
，C正确，即克服摩擦力做功为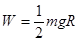，D错误，
考点：考查了平抛运动已经动能定理的应用
点评：本题的突破口为; 在B点小球恰好对轨道没有压力,求出B点的速度，
练习册系列答案
相关题目
（2008?广州二模）如图所示，在竖直平面内有水平向右的匀强电场，同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球，另一端固定于0点，已知带电小球受到的电场力大于重力，小球由静止释放，到达图中竖直虚线前小球做（ ）
如图所示，在竖直平面内有一边长为L的正方形区域处在场强为E的匀强电场中，电场方向与正方形一边平行．一质量为m、带电量为q的小球由某一边的中点，以垂直于该边的水平初速V0进入该正方形区域．当小球再次运动到该正方形区域的边缘时，具有的动能可能为（ ）
如图所示，在竖直平面内有一半圆形轨道，圆心为O，一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出，落于圆轨道上的C点，已知OC的连线与OA的夹角为θ，求小球从A到C的时间t=？（空气阻力不计）
如图所示，在竖直平面内有一个粗糙的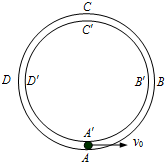
如图所示，在竖直平面内固定两个很靠近的同心圆形轨道，外轨道ABCD光滑，内轨道A′B′C′D′的上半部分B′C′D′粗糙，下半部分B′A′D′光滑，一质量m=0.2kg的小球从轨道的最低点A，以初速度v0向右运动，球的尺寸略小于两圆间距，已知圆形轨道的半径R=0.32m，取g=10m/s2．