题目内容
如图所示,两个 圆弧轨道固定在水平面上,半径为R,不计一切摩擦.将A、B两小球分别从两轨道右侧正上方静止下落,若设小球释放时距离地面的高度为hA和hB,试求
圆弧轨道固定在水平面上,半径为R,不计一切摩擦.将A、B两小球分别从两轨道右侧正上方静止下落,若设小球释放时距离地面的高度为hA和hB,试求(1)要使小球能够运动到最高点,则A、B两小球离地面的高度hA和hB有何要求
(2)能否使小球能够从最高点飞出后又恰好落在轨道的右端口,若能,则离地面的高度是多少;若不能,说明理由.

【答案】分析:(1)A小球能够运动到最高点的要求是最高点速度不小于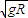 ,B小球能到达最高点的临界要求是速度为零;然后根据机械能守恒定律列式求解;
,B小球能到达最高点的临界要求是速度为零;然后根据机械能守恒定律列式求解;
(2)先根据平抛运动的知识求得圆轨道最高点速度,然后根据机械能守恒定律计算释放点离地的高度.
解答:解:(1)小球能够运动到最高点的最小速度要求分别是:
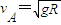 ;vB=0 ①
;vB=0 ①
所以由机械能守恒定律得
mg(hA-2R)=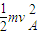 ②
②
mg(hB-2R)=0 ③
解得:hA=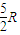 ;hB=2R ④
;hB=2R ④
即要使小球能够运动到最高点,A、B两个小球离地面的高度要求分别是hA≥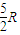 ,hB≥2R.
,hB≥2R.
(2)使小球能够从最高点飞出后又恰好落在轨道的右端口,即刚好做平抛运动,有
R=vt,R=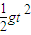 ⑤
⑤
得v=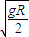 <vA ⑥
<vA ⑥
所以此速度不能使A小球从最高点飞出后又恰好落在轨道的右端口,而使B小球从最高点飞出后又恰好落在轨道的右端口
mg(hB-2R)=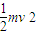
得hB=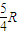
即A小球不能从最高点飞出后又恰好落在轨道的右端口,而使B小球能从最高点飞出后又恰好落在轨道的右端口,释放点离地高度为 R.
R.
点评:本题关键计算出小球能到圆轨道最高点的速度,然后根据机械能守恒定律和平抛运动的位移公式列式求解.
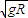 ,B小球能到达最高点的临界要求是速度为零;然后根据机械能守恒定律列式求解;
,B小球能到达最高点的临界要求是速度为零;然后根据机械能守恒定律列式求解;(2)先根据平抛运动的知识求得圆轨道最高点速度,然后根据机械能守恒定律计算释放点离地的高度.
解答:解:(1)小球能够运动到最高点的最小速度要求分别是:
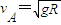 ;vB=0 ①
;vB=0 ①所以由机械能守恒定律得
mg(hA-2R)=
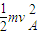 ②
②mg(hB-2R)=0 ③
解得:hA=
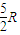 ;hB=2R ④
;hB=2R ④即要使小球能够运动到最高点,A、B两个小球离地面的高度要求分别是hA≥
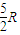 ,hB≥2R.
,hB≥2R.(2)使小球能够从最高点飞出后又恰好落在轨道的右端口,即刚好做平抛运动,有
R=vt,R=
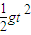 ⑤
⑤得v=
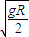 <vA ⑥
<vA ⑥所以此速度不能使A小球从最高点飞出后又恰好落在轨道的右端口,而使B小球从最高点飞出后又恰好落在轨道的右端口
mg(hB-2R)=
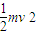
得hB=
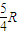
即A小球不能从最高点飞出后又恰好落在轨道的右端口,而使B小球能从最高点飞出后又恰好落在轨道的右端口,释放点离地高度为
 R.
R.点评:本题关键计算出小球能到圆轨道最高点的速度,然后根据机械能守恒定律和平抛运动的位移公式列式求解.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
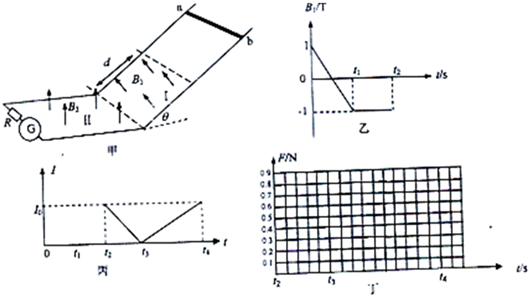
 角,倾斜导轨的下面部分处在一垂直斜面的匀强磁场区I中,I区中磁场的磁感应强度B1随时间变化的规律如图(乙)所示垂直斜面向上为正值,图中t1、t2未知。水平导轨足够长,其左端接有理想灵敏电流计G(内阻不计)和定值电阻R=3
角,倾斜导轨的下面部分处在一垂直斜面的匀强磁场区I中,I区中磁场的磁感应强度B1随时间变化的规律如图(乙)所示垂直斜面向上为正值,图中t1、t2未知。水平导轨足够长,其左端接有理想灵敏电流计G(内阻不计)和定值电阻R=3 ,水平导轨处在一竖直向上的匀强磁场区Ⅱ中,Ⅱ区中的磁场恒定不变,磁感应强度大小为B2=1T,在t=0时刻,从斜轨上磁场I区外某处垂直于导轨水平静止释放一金属棒ab,棒的质量m=0.l kg,棒的电阻r=2
,水平导轨处在一竖直向上的匀强磁场区Ⅱ中,Ⅱ区中的磁场恒定不变,磁感应强度大小为B2=1T,在t=0时刻,从斜轨上磁场I区外某处垂直于导轨水平静止释放一金属棒ab,棒的质量m=0.l kg,棒的电阻r=2
 角,倾斜导轨的下面部分处在一垂直斜面的匀强磁场区I中,I区中磁场的磁感应强度B1随时间变化的规律如图(乙)所示垂直斜面向上为正值,图中t1、t2未知。水平导轨足够长,其左端接有理想灵敏电流计G(内阻不计)和定值电阻R=3
角,倾斜导轨的下面部分处在一垂直斜面的匀强磁场区I中,I区中磁场的磁感应强度B1随时间变化的规律如图(乙)所示垂直斜面向上为正值,图中t1、t2未知。水平导轨足够长,其左端接有理想灵敏电流计G(内阻不计)和定值电阻R=3 ,水平导轨处在一竖直向上的匀强磁场区Ⅱ中,Ⅱ区中的磁场恒定不变,磁感应强度大小为B2=1T,在t=0时刻,从斜轨上磁场I区外某处垂直于导轨水平静止释放一金属棒ab,棒的质量m=0.l kg,棒的电阻r=2
,水平导轨处在一竖直向上的匀强磁场区Ⅱ中,Ⅱ区中的磁场恒定不变,磁感应强度大小为B2=1T,在t=0时刻,从斜轨上磁场I区外某处垂直于导轨水平静止释放一金属棒ab,棒的质量m=0.l kg,棒的电阻r=2
