题目内容
 (2013?辽宁一模)“∟”形轻杆两边互相垂直、长度均为l,可绕过O点的水平轴在竖直平面内自由转动,两端各固定一个金属小球A、B,其中A球质量为m,带负电,电量为q(q>0),B球开始不带电,质量未知.现将“∟”形杆从OB位于水平位置由静止释放.(sin37°=0.6,cos37°=0.8)
(2013?辽宁一模)“∟”形轻杆两边互相垂直、长度均为l,可绕过O点的水平轴在竖直平面内自由转动,两端各固定一个金属小球A、B,其中A球质量为m,带负电,电量为q(q>0),B球开始不带电,质量未知.现将“∟”形杆从OB位于水平位置由静止释放.(sin37°=0.6,cos37°=0.8)(1)当OB杆转过37°时,两球的速度达到最大,则B球的质量为多少?
(2)若在空间加一竖直向下的匀强电场,OB杆从原来位置开始释放能转过的最大角度为127°,则该电场的电场强度大小为多少?
分析:(1)在整个过程中,只有重力做功,系统机械能守恒,由机械能守恒定律可以求出B球的质量;
(2)在整个过程中,重力与电场力做功,由能量守恒定律可以求出电场强度的大小.
(2)在整个过程中,重力与电场力做功,由能量守恒定律可以求出电场强度的大小.
解答:解:(1)两球组成的系统动量守恒,由机械能守恒可知,动能最大时,重力势能最小,
由机械能守恒定律得:
△Ep=mBgl?sinθ-mAgl(1-cosθ)=(mBsinθ+mAcosθ)gl-mAgl;
由数学规律可知:△Ep=[
sin(θ+?)-mA]gl,其中tan?=
,
由题意可知,当θ=37°即?=53°时动能最大,可得:mB=
mA=
m;
(2)到达最大角度时,动能为零,由能量守恒定律得:
mAgl(1+sin37°)-mBglcos37°=Eql(1+sin37°),解得:E=
;
答:(1)B球的质量
mg;
(2)该电场的电场强度大小为
.
由机械能守恒定律得:
△Ep=mBgl?sinθ-mAgl(1-cosθ)=(mBsinθ+mAcosθ)gl-mAgl;
由数学规律可知:△Ep=[
| mB2+mA2 |
| mA |
| mB |
由题意可知,当θ=37°即?=53°时动能最大,可得:mB=
| 3 |
| 4 |
| 3 |
| 4 |
(2)到达最大角度时,动能为零,由能量守恒定律得:
mAgl(1+sin37°)-mBglcos37°=Eql(1+sin37°),解得:E=
| 5mg |
| 8q |
答:(1)B球的质量
| 3 |
| 4 |
(2)该电场的电场强度大小为
| 5mg |
| 8q |
点评:本题考查了求球的质量、电场强度等问题,应用机械能守恒定律、能量守恒定律即可正确解题,本题的难点是数学知识的应用;另外本题也可以应用杠杆平衡条件分析答题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?辽宁一模)我国国家大剧院外部呈椭球形.假设国家大剧院的屋顶为半球形,一警卫人员为执行特殊任务,必须冒险在半球形屋顶向上缓慢爬行,他在向上爬的过程中( )
(2013?辽宁一模)我国国家大剧院外部呈椭球形.假设国家大剧院的屋顶为半球形,一警卫人员为执行特殊任务,必须冒险在半球形屋顶向上缓慢爬行,他在向上爬的过程中( )
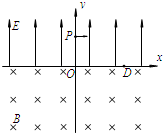 (2013?辽宁一模)在如图所示的xoy坐标系中,y>0的区域内存在着沿y轴正方向、场强为E的匀强电场,y<0的区域内存在着垂直纸面向里、磁感应强度为B的匀强磁场.一带电粒子从y轴上的P(0,h)点以沿x轴正方向的初速度射出,恰好能通过x轴上的D(d,0)点.已知带电粒子的质量为m,带电量为-q.h、d、q均大于0,不计重力的影响.
(2013?辽宁一模)在如图所示的xoy坐标系中,y>0的区域内存在着沿y轴正方向、场强为E的匀强电场,y<0的区域内存在着垂直纸面向里、磁感应强度为B的匀强磁场.一带电粒子从y轴上的P(0,h)点以沿x轴正方向的初速度射出,恰好能通过x轴上的D(d,0)点.已知带电粒子的质量为m,带电量为-q.h、d、q均大于0,不计重力的影响.