如图所示.直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域.磁感应强度为B.质子从O点以与MN成60度角的速度v射入该磁场区域.经一段时间后从边界MN射出．求:(1)它从磁场中射出时.离出射点间的距离,(2)它在磁场中运动的时间．题目和参考答案——青夏教育精英家教网—

题目内容

如图所示，直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域，磁感应强度为B，质子从O点以与MN成60度角的速度v射入该磁场区域（电子质量为m，电量为e），经一段时间后从边界MN射出．求：
（1）它从磁场中射出时，离出射点间的距离；
（2）它在磁场中运动的时间．

分析：粒子做匀速圆周运动，由洛仑兹力充当向心力可知粒子离开磁场时的距离，则可求出出射点的距离；根据粒子在磁场中转动的圆心角可知时间．

解答：解：（1）质子在磁场中做匀速圆周运动，洛伦兹力充当向心力：
eVB=

mV2

所以R=

由图象知出射点间的距离为L=2Rsin60°=

（2）质子在磁场中的圆心角为120°，所以在磁场中运动的时间t=

120

360

2πm

3eB

答：（1）它从磁场中射出时，离出射点间的距离

；
（2）它在磁场中运动的时间

2πm

3eB

．

点评：带电粒子在电场中的运动关键在于由几何关系找出圆心和半径，再由洛仑兹力充当向心力及圆的性质可得出几何关系及转动时间．

练习册系列答案

相关题目

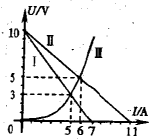（1）如图所示，直线I、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的图线，曲线Ⅲ是一个小灯泡的伏安特性曲线，则电源1和电源2的内阻之比为

11：7

．若把该小灯泡先后分别与电源1和电源2单独连接时，则在这两种连接状态下，小灯泡消耗的功率之比为

1：2

．
（2）某学生用螺旋测微器在测定某一金属丝的直径时，测得的结果如图甲所示，则该金属丝的直径d=

2.706

mm．另一位学生用游标尺上标有20等分刻度的游标卡尺测一工件的长度，测得的结果如图乙所示，则该工件的长度L=

5.015

cm．

（3）如图所

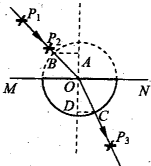示，某同学用插针法测定一半圆形玻璃砖的折射率，在平铺的白纸上垂直纸面插大头针P₁、P₂确定入射光线，
并让入射光线过圆心O，在玻璃砖（图中实线部分）另一侧垂直纸面插大头针P₃，使P₃挡住P₁、P₂的像，连接OP₃．图中MN为分界面，虚线半圆与玻璃砖对称，B、C分别是入射光线、折射光线与圆的交点，AB、CD均垂直于法线并分别交法线于A、D点．设AB的长度为l₁，AO的长度为l₂，CD的长度为l₃，DO的长度为l₄，圆的半径为R，为较方便地表示出玻璃砖的折射率，需用刻度尺测量的是

l₁、l₃．

（用上述所给物理量的字母表示），则玻璃砖的折射率可表示为

．
（4）在“用多用表测电阻”的实验中，下列说法中正确的是

A．测电阻时，红、黑表笔分别错插入负、正插孔，只要其它方法正确，不影响被测量电阻的结果
B．测量阻值不同的电阻时都必须重新调零
C．用×1的欧姆档测量时，指针恰好指示在10Ω与20Ω正中间，所测电阻的阻值一定小于15Ω
D．多用表使用完毕后，应将选择开关置于欧姆表最大档，以防表头烧坏．

(20分)如图所示，直线MN上方存在着垂直纸面向里、磁感应强度为B的匀强磁场，质量为m、电荷量为-q(q>0)的粒子1以速度v1=v0从O点垂直射入磁场，其方向与MN的夹角=30o；质量为m、电荷量为+q的粒子2以速度也从O点垂直射入磁场，其方向与MN的夹角=60o。已知粒子l、2同时到达磁场边界的A、B两点(图中未画出)，不计粒子的重力及粒子间的相互作用。

(1)请画出粒子1和2在磁场中运动的轨迹；

(2)求两粒子在磁场边界上的穿出点A、B之间的距离d；

(3)求两粒子进入磁场的时间间隔t；

(4)若MN下方有一匀强电场，使两粒子在电场中相遇，其中的粒子1做匀加速直线运动。求电场强度E的大小。

（18分）如图所示，直线MN上方存在着垂直纸面向里、磁感应强度为B的匀强磁场，质量为m、电荷量为-q（q＞0）的粒子1在纸面内以速度从O点射入磁场，其方向与MN的夹角α=30°；质量为m、电荷量为+q的粒子2在纸面内以速度也从O点射入磁场，其方向与MN的夹角β=60°角。已知粒子1、2同时到达磁场边界的A、B两点（图中未画出），不计粒子的重力及粒子间的相互作用。

（1）求两粒子在磁场边界上的穿出点A、B之间的距离d；

（2）求两粒子进入磁场的时间间隔；

（3）若MN下方有平行于纸面的匀强电场，且两粒子在电场中相遇，其中的粒子1做直线运动。求电场强度E的大小和方向。

如图所示，直线MN表示一条平直公路，甲、乙两辆汽车原来停在A、B两处，A、B间的距离为85m，现甲车先开始向右做匀加速直线运动，加速度a₁＝2.5m/s²，甲车运动6.0s时，乙车立即开始向右做匀加速直线运动，加速度a₂＝5.0m/s²，求:

（1）乙车运动多长时间被甲车追上？

（2）两辆汽车相遇处距A处的距离。

如图所示,在直线MN上方有垂直纸面向里的匀强磁场，一质量为m、带电荷量为q的粒子，沿与MN成45°角的方向由O点垂直于磁场方向飞入磁场，ts后达到MN直线上的某一点P，OP=r，则该带电粒子带______________，匀强磁场的磁感应强度为______________，粒子的速度为______________.

试题分类