题目内容
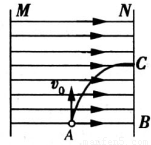如图所示，M、N是竖直放置的两平行金属板，分别带等量异种电荷，两极间产生一个水平向右的匀强电场，场强为E，一质量为m、电荷量为+q的微粒，以初速度v竖直向上从两极正中间的A点射入匀强电场中，微粒垂直打到N极上的C点，已知AB=BC．不计空气阻力，则可知（ ）A．微粒在电场中作类平抛运动
B．微粒打到C点时的速率与射入电场时的速率相等
C．MN板间的电势差为m
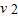/qD．MN板间的电势差为E
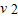/2g
【答案】分析：根据类平抛运动的特点：初速度的方向与合外力的方向垂直来判定粒子是否在电场中做类平抛运动，根据动能定理判定粒子达到C点是的速度，和MN之间的电势差．
解答：解：A：因电场力和重力均为恒力，其合力亦为恒力，且与v有一定夹角，故微粒做匀变速曲线运动--即抛物线运动，但不是类平抛运动，所以A错．
B：因AB=BC，即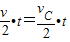
可见vC=v．故B项正确；
C：由动能定理，得：W电+WG=△Ek=0，即：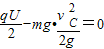
，所以：
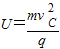，故C项正确；
D：由mg=qE得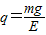
代入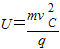
，
得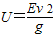
，故D项错误．
故选：BC
点评：该题中根据类平抛运动的特点来判定粒子是否在电场中做类平抛运动是解题的关键，动能定理判定粒子达到C点是的速度，和MN之间的电势差相对比较简单．属于基础题目．
解答：解：A：因电场力和重力均为恒力，其合力亦为恒力，且与v有一定夹角，故微粒做匀变速曲线运动--即抛物线运动，但不是类平抛运动，所以A错．
B：因AB=BC，即
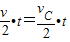可见vC=v．故B项正确；C：由动能定理，得：W电+WG=△Ek=0，即：
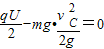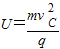，所以：，故C项正确；D：由mg=qE得
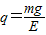代入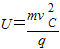，得
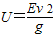，故D项错误．故选：BC
点评：该题中根据类平抛运动的特点来判定粒子是否在电场中做类平抛运动是解题的关键，动能定理判定粒子达到C点是的速度，和MN之间的电势差相对比较简单．属于基础题目．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
如图所示，M、N是竖直放置的两平行金属板，分别带等量异种电荷，两极间产生一个水平向右的匀强电场，场强为E，一质量为m、电量为+q的微粒，以初速度v0竖直向上从两极正中间的A点射入匀强电场中，微粒垂直打到N极上的C点，已知AB=BC．不计空气阻力，则可知（ ）
如图所示，M、N是竖直放置的平行板电容器的两个极板，R0为定值电阻，R1、R2为可调电阻，用绝缘细线将质量为m、电荷量为+q的小球悬于电容器内部，闭合开关后，小球处于静止状态，现要使小球静止时细线与竖直方向的夹角变大（始终不与极板接触），正确操作的是（ ）
如图所示，M、N是竖直放置的两平行金属板，分别带等量异种电荷，两极板间产生一个水平向右的匀强电场，场强为E，一质量为m、电荷量为+q的微粒，以初速度v0竖直向上从两极正中间的A点射入匀强电场中，微粒垂直打到N极板上的C点，已知AB=BC．不计空气阻力，则可知（ ）| A、微粒在电场中做抛物线运动 | ||
| B、微粒打到C点时的速率与射入电场时的速率相等 | ||
C、MN板间的电势差为2m
| ||
D、MN板间的电势差为E
|
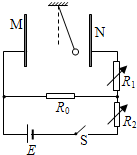如图所示，M、N是竖直放置的平行板电容器的两个极板，R0为定值电阻，R1、R2为可调电阻，用绝缘细线将质量为m、电荷量为+q的小球悬于电容器内部．闭合开关S，设法让小球做小角度摆动，测得周期为T．调节R1、R2，关于该摆做小角度振动的周期的判断，正确的是（小球摆动时不会碰极板）（ ）