题目内容
如图所示，倾角为θ的斜面上静止放置三个质量均为m的木箱，相邻两木箱的距离均为l．工人用沿斜面的力推最下面的木箱使之上滑，逐一与其它木箱碰撞．每次碰撞后木箱都粘在一起运动．整个过程中工人的推力不变，最后恰好能推着三个木箱匀速上滑．已知木箱与斜面间的动摩擦因数为μ，重力加速度为g．设碰撞时间极短，求
（1）工人的推力；
（2）三个木箱匀速运动的速度；
（3）在第一次碰撞中损失的机械能．
（1）工人的推力；
（2）三个木箱匀速运动的速度；
（3）在第一次碰撞中损失的机械能．
（1）当匀速时，把三个物体看作一个整体受重力、推力F、摩擦力f和支持力．
根据平衡的知识有
F=3mgsinθ+3μmgcosθ．
（2）第一个木箱与第二个木箱碰撞之前的速度为V1，加速度a1=
=2g（sinθ+μcosθ）
根据运动学公式或动能定理有V1=2
，
碰撞后的速度为V2根据动量守恒有mV1=2mV2，即碰撞后的速度为V2=
，
然后一起去碰撞第三个木箱，设碰撞前的速度为V3
从V2到V3的加速度为a2=
=
，
根据运动学公式有V32-V22=2a2L，得
V3=
，
跟第三个木箱碰撞根据动量守恒有2mV3=3mV4，得
V4=
，就是匀速的速度．
（3）设第一次碰撞中的能量损失为△E，根据能量守恒有
mV12=△E+
?2mV22，带入数据得
△E=mgL（sinθ+μcosθ）．
答：（1）工人的推力为F=3mgsinθ+3μmgcosθ．
（2）三个木箱匀速运动的速度为
．
（3）在第一次碰撞中损失的机械能mgL（sinθ+μcosθ）．
根据平衡的知识有
F=3mgsinθ+3μmgcosθ．
（2）第一个木箱与第二个木箱碰撞之前的速度为V1，加速度a1=
| F-mgsinθ-μmgcosθ |
| m |
根据运动学公式或动能定理有V1=2
| gL(sinθ+μcosθ) |
碰撞后的速度为V2根据动量守恒有mV1=2mV2，即碰撞后的速度为V2=
| gL(sinθ+μcosθ) |
然后一起去碰撞第三个木箱，设碰撞前的速度为V3
从V2到V3的加速度为a2=
| F-2mgsinθ-2μmgcosθ |
| 2m |
| g(sinθ+μcosθ) |
| 2 |
根据运动学公式有V32-V22=2a2L，得
V3=
| 2gL(sinθ+μcosθ) |
跟第三个木箱碰撞根据动量守恒有2mV3=3mV4，得
V4=
| 2 |
| 3 |
| 2gL(sinθ+μcosθ) |
（3）设第一次碰撞中的能量损失为△E，根据能量守恒有
| 1 |
| 2 |
| 1 |
| 2 |
△E=mgL（sinθ+μcosθ）．
答：（1）工人的推力为F=3mgsinθ+3μmgcosθ．
（2）三个木箱匀速运动的速度为
| 2 |
| 3 |
| 2gL(sinθ+μcosθ) |
（3）在第一次碰撞中损失的机械能mgL（sinθ+μcosθ）．
练习册系列答案
相关题目
（2013?淮安模拟）如图所示，倾角为37°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相连，O为轨道圆心，BC为圆轨道直径且处于竖直方向，A、C两点等高．质量m=1kg的滑块从A点由静止开始下滑，恰能滑到与O等高的D点，g取10m/s2，sin37°=0.6，cos37°=0.8．
如图所示，倾角为30°的光滑固定斜面，质量分别为m1和m2的两个滑块用不可伸长的轻绳通过滑轮连接（不计滑轮的质量和摩擦），将两滑块由静止释放，m1静止，此时绳中的张力为T1．若交换两滑块的位置，再由静止释放，此时绳中的张力为T2，则T1与T2的比值为（ ）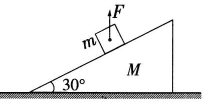
如图所示，倾角为θ=30°的斜面体静止固定在水平面上，现将一个重为30N的物体m，放在该斜面体上静止不动，若用F=5N的拉力竖直向上提物体，物体仍静止，下述结论正确的是（ ）
如图所示，倾角为37°的传送带以4m/s的速度沿图示方向匀速运动．已知传送带的上、下两端间的距离为L=7m．现将一质量m=0.4kg的小木块轻放到传送带的顶端，使它从静止开始沿传送带下滑，已知木块与传送带间的动摩擦因数为μ=0.25，设最大静摩擦力等于滑动摩擦力，取g=10m/s2．求：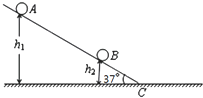
如图所示，倾角为37°的足够长粗糙斜面下端与一足够长光滑水平面相接，斜面上有两小球A、B，距水平面高度分别为h1=5.4m和h2=0.6m．现由静止开始释放A球，经过一段时间t后，再由静止开始释放B球．A和B与斜面之间的动摩擦因素均为μ=0.5，重力加速度g=10m/s2，不计空气阻力，设小球经过斜面和水平面交界处C机械能不损失，（sin37°=0.6，cos37°=0.8）． 求：