题目内容
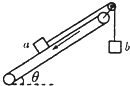
【题目】如图所示，
是倾角为30°的光滑固定斜面．劲度系数为
的轻弹簧一端固定在斜面底端的固定挡板
上，另一端与质量为
的物块
相连接．细绳的一端系在物体上，细绳跨过不计质量和摩擦的定滑轮，另一端有一个不计质量的小挂钩．小挂钩不挂任何物体时，物体处于静止状态，细绳与斜面平行．在小挂钩上轻轻挂上一个质量也为的物块
后，物块沿斜面向上运动．斜面足够长，运动过程中始终未接触地面．已知重力加速度为
，求：
（1）物块处于静止时，弹簧的压缩量
（2）设物块沿斜面上升通过
点位置时速度最大，求点到出发点的距离
和最大速度
；
（3）把物块的质量变为原来的
倍(>0.5)，小明同学认为，只要足够大，就可以使物块沿斜面上滑到点时的速度增大到2，你认为是否正确？如果正确，请说明理由，如果不正确，请求出沿斜面上升到点位置的速度的范围．
【答案】（1）mg/2k （2）
（3） 
【解析】（1）小挂钩不挂任何物体时，物体A处于静止状态，由平衡条件得：
得：
，
（2）当A受到的合力为零时速度最大，此时：
，
解得：
，
Q点到出发点的距离：
；
在出发点与Q弹簧的形变量相同，弹簧的弹性势能相等，
由机械能守恒定律得：
，
解得，最大速度：
；
（4）B的质量变为Nm时，由机械能守恒定律得：
，
解得：
，
N→∞时，
，
由于N不会达到无穷大，因此速度不会达到
，
小明的说法是错误的，速度范围是：
练习册系列答案
相关题目
