题目内容
如图所示，固定在竖直平面的光滑绝缘圆环处于匀强电场中，场强方向与圆环平面平行且与水平方向成30°，环上与圆心O等高的A点套有一个质量为m，电荷量为+q的小球恰好处于平衡状态．（重力加速度为g），求：（1）匀强电场的场强大小
（2）某时刻突然将电场方向变为竖直向下，场强大小不变，小球滑到最低点B时对环的压力大小．
分析：（1）小球处于平衡状态时，合外力为零，分析受力情况，根据平衡条件列式求解场强大小．
（2）突然将电场方向变为竖直向下，场强大小不变，电场力大小不变，方向变为竖直向下，小球将向下加速运动，先根据动能定理求得小球到达最低点时的速率，再根据牛顿第二定律求出轨道对小球的支持力，即可得到小球对环的压力．
（2）突然将电场方向变为竖直向下，场强大小不变，电场力大小不变，方向变为竖直向下，小球将向下加速运动，先根据动能定理求得小球到达最低点时的速率，再根据牛顿第二定律求出轨道对小球的支持力，即可得到小球对环的压力．
解答：
解：（1）小球处于平衡状态时，分析小球的受力情况如图，根据平衡条件得：
Eqsin30°=mg…①
得场强大小为 E=
．
（2）突然将电场方向变为竖直向下后，小球将向下运动，从A到B的过程，由动能定理得：
(Eq+mg)R=
mv2…②
在最低点，由牛顿第二定律得 N-(Eq+mg)=
…③
由②③得 N=9mg
由牛顿第三定律得，小球对环的压力大小为 F压=N=9mg
答：
（1）匀强电场的场强大小是
．
（2）某时刻突然将电场方向变为竖直向下，场强大小不变，小球滑到最低点B时对环的压力大小是9mg．
解：（1）小球处于平衡状态时，分析小球的受力情况如图，根据平衡条件得：Eqsin30°=mg…①
得场强大小为 E=
| 2mg |
| q |
（2）突然将电场方向变为竖直向下后，小球将向下运动，从A到B的过程，由动能定理得：
(Eq+mg)R=
| 1 |
| 2 |
在最低点，由牛顿第二定律得 N-(Eq+mg)=
| mv2 |
| R |
由②③得 N=9mg
由牛顿第三定律得，小球对环的压力大小为 F压=N=9mg
答：
（1）匀强电场的场强大小是
| 2mg |
| q |
（2）某时刻突然将电场方向变为竖直向下，场强大小不变，小球滑到最低点B时对环的压力大小是9mg．
点评：本题是平衡条件、动能定理和向心力知识的综合应用，分析向心力的来源是求解的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，固定在竖直平面半径为R的光滑圆环，有质量为m的小球在轨道内侧作圆周运动，小球恰好能通过圆环的最高点．已知重力加速度为g，则小球在运动过程（ ）
如图所示，固定在竖直平板且不可伸长的绝缘轻绳栓一质量为m、电量为q的小球（可视为点电荷），小球平衡时与固定在平板的点电荷Q的连线恰好水平．若小球的质量变为2m时，而其位置仍要保持不变，则小球的电量应该变为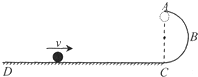
计，g取10m/s2．
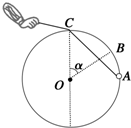如图所示，固定在竖直平面内的半径为R=0.5m的光滑圆环的最高点C处有一个光滑的小孔，一质量为m=0.1kg的小球套在圆环上，一根细线的一端拴着这个小球，细线的另一端穿过小孔C，手拉细线使小球从A处沿圆环向上移动．在下列两种情况下，当小球通过B处，即∠COB=α=740时，求这两种情况下，细线对小球的拉力F的大小和圆环对小球的弹力FN的大小．（不计空气阻力，g取10m/s2；sin37°=0.6，cos37°=0.8；可能用到