题目内容
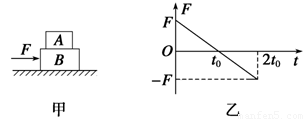
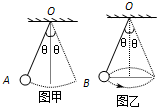如图甲、图乙所示，A、B两小球质量相等，悬挂两球的线长也相同，A在竖直平面内摆动，最大摆角为θ，B作匀速圆锥摆运动，锥的顶角为2θ，θ＜100，则A、B两球运动的周期之比T1：T2以及在图示位置时细线中的拉力之比FA：FB为（ ）分析：图甲中小球做单摆的运动，图乙中小球做圆锥摆．根据单摆的周期公式求出小球A的周期，根据合力提供向心力求出B的周期，从而求出周期之比．
在图示位置，A球在沿绳子方向上的合力为零，运用正交分解求出绳子的拉力，对于B球，根据合力指向圆心，通过平行四边形定则求出绳子的拉力．
在图示位置，A球在沿绳子方向上的合力为零，运用正交分解求出绳子的拉力，对于B球，根据合力指向圆心，通过平行四边形定则求出绳子的拉力．
解答：解：对于A球：TA=2π
，根据正交分解得，由于沿绳子方向上的合力为零，则FA=mgcosθ．
对于B球：mgtanθ=mlsinθ
，解得TB=2π
．绳子的拉力FB=
．
则
=
，
=
．故C正确，A、B、D错误．
故选C．
|
对于B球：mgtanθ=mlsinθ
| 4π2 |
| T2 |
|
| mg |
| cosθ |
则
| TA |
| TB |
|
| FA |
| FB |
| cos2θ |
| 1 |
故选C．
点评：解决本题的关键知道圆锥摆和单摆的区别，知道小球做圆周运动向心力的来源，运用牛顿第二定律进行求解．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
