题目内容
一电梯启动时匀加速上升,加速度为1.2m/s2,制动后匀减速上升,加速度为-1m/s2,电梯上升的最大速度为6m/s,则电梯启动后加速的时间不超过 s;电梯到达51m顶层的最短时间为 s.
【答案】分析:电梯经历先加速、后匀速、再减速的运动过程.匀速时的速度为最大速度v,这样时间才能最短.根据运动速度公式和位移公式求解出匀加速运动的时间、匀减速运动的时间、匀速运动的位移、匀减速运动的位移.而匀加速运动的位移为6t2,根据总位移x=x1+x2+x3,代入数据可解得t2.故总时间即最短时间为t=t1+t2+t3.
解答:解:电梯经历先加速、后匀速、再减速的运动过程.
设加速时加速度a1,时间t1;减速加速度a3,时间t3,最大速度为v,则匀速时的速度为最大速度v,这样时间才能最短.
匀加速运动的时间t1=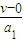 =
=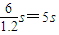 ,
,
匀减速运动的时间t3=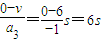
匀加速运动的位移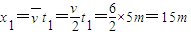
匀速运动的位移x2=vt2=6t2
匀减速运动的位移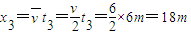
总位移x=x1+x2+x3
代入数据51=15+6t2+18
解得t2=3s
所以总时间即最短时间为t=t1+t2+t3=5s+3s+6s=14s.
故答案为:5,14.
点评:解决本题的关键熟练掌握匀变速直线运动的速度公式和位移公式,以及平均速度公式.
解答:解:电梯经历先加速、后匀速、再减速的运动过程.
设加速时加速度a1,时间t1;减速加速度a3,时间t3,最大速度为v,则匀速时的速度为最大速度v,这样时间才能最短.
匀加速运动的时间t1=
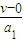 =
=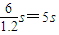 ,
,匀减速运动的时间t3=
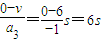
匀加速运动的位移
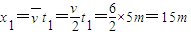
匀速运动的位移x2=vt2=6t2
匀减速运动的位移
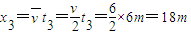
总位移x=x1+x2+x3
代入数据51=15+6t2+18
解得t2=3s
所以总时间即最短时间为t=t1+t2+t3=5s+3s+6s=14s.
故答案为:5,14.
点评:解决本题的关键熟练掌握匀变速直线运动的速度公式和位移公式,以及平均速度公式.

练习册系列答案
相关题目
一位同学家住在24层高楼的顶楼,他想研究一下电梯上升的运动过程.乘电梯上楼时捎带了一个质量未知的砝码和一个量程足够大的弹簧测力计,用手提着弹簧测力计,砝码悬挂在测力计钩上.电梯从一层开始启动,中间不间断,一直到最高层停止.在这个过程中,他记录了弹簧测力计在不同时段内的读数如下表所示:(取g=10m/s2)
| 时间t/s | 弹簧测力计示数F/N |
| 电梯启动前 | 50.0 |
| 匀加速阶段(0-3.0) | 58.0 |
| 匀速阶段(3.0-13.0) | 50.0 |
| 匀减速阶段(13.0-19.0) | 46.0 |
| 19.0以后 | 50.0 |
(3)电梯匀速上升时的速度大小;(4)该同学居住的房间距一层地面的高度.
(8分)一同学家住在24层高楼的顶楼,他想研究一下电梯上升的运动过程。乘电梯上楼时携带了一个质量未知的砝码和一个量程足够大的弹簧测力计,用手提着弹簧测力计,砝码悬挂在测力计钩上。电梯从一层开始启动,中间不间断,一直到最高层停止。在这个过程中,他记录了弹簧测力计在不同时段内的读数如下表所示:
时间t/s | 弹簧测力计示数F/N |
电梯启动前 | 50.0 |
匀加速阶段(0~3.0) | 58.0 |
匀速阶段(3.0~13.0) | 50.0 |
匀减速阶段(13.0~19.0) | 46.0 |
19.0以后 | 50.0 |
根据表中数据求:(取g=10m/s2)
(1)砝码的质量;
(2)电梯在加速阶段的加速度大小;
(3)电梯匀速上升时的速度大小;
(4)该同学居住的房间距一层地面的高度。
一位同学家住在24层高楼的顶楼,他想研究一下电梯上升的运动过程.乘电梯上楼时捎带了一个质量未知的砝码和一个量程足够大的弹簧测力计,用手提着弹簧测力计,砝码悬挂在测力计钩上.电梯从一层开始启动,中间不间断,一直到最高层停止.在这个过程中,他记录了弹簧测力计在不同时段内的读数如下表所示:(取g=10m/s2)
根据表中数据求;(1)砝码的质量;(2)电梯在加速阶段的加速度大小;
(3)电梯匀速上升时的速度大小;(4)该同学居住的房间距一层地面的高度.
| 时间t/s | 弹簧测力计示数F/N |
| 电梯启动前 | 50.0 |
| 匀加速阶段(0-3.0) | 58.0 |
| 匀速阶段(3.0-13.0) | 50.0 |
| 匀减速阶段(13.0-19.0) | 46.0 |
| 19.0以后 | 50.0 |
(3)电梯匀速上升时的速度大小;(4)该同学居住的房间距一层地面的高度.