题目内容
7. 长为6L、质量为6m的匀质绳,置于特制的水平桌面上,绳的一端悬垂于桌边外,另一端系有一个可视为质点的质量为15m的木块,如图所示.木块在AB段与桌面无摩擦,在BE段与桌面有摩擦,匀质绳与桌面的摩擦可忽略.初始时刻用手按住木块使其停在A处,绳处于绷紧状态,AB=BC=CD=DE=L,放手后,木块最终停在C处.桌面距地面高度大于6L.
长为6L、质量为6m的匀质绳,置于特制的水平桌面上,绳的一端悬垂于桌边外,另一端系有一个可视为质点的质量为15m的木块,如图所示.木块在AB段与桌面无摩擦,在BE段与桌面有摩擦,匀质绳与桌面的摩擦可忽略.初始时刻用手按住木块使其停在A处,绳处于绷紧状态,AB=BC=CD=DE=L,放手后,木块最终停在C处.桌面距地面高度大于6L.(1)求木块刚滑至B点时的速度v和木块与BE段的动摩擦因数μ;
(2)若木块在BE段与桌面的动摩擦因数变为μ′=0.35,则木块最终停在何处?
分析 (1)对木块从A到B段运用动能定理,求出木块滑至B点的速度大小,对木块从A滑至C过程中,由能量守恒定律求出动摩擦因数.
(2)假设木块运动一段后停止的位移,则由功能关系,结合题意可得运动的位移,从而确定木块停在何处;
解答 解:(1)木块从A滑至B过程中,由动能定理得:3mg•$\frac{3}{2}$L-2mg•L=$\frac{1}{2}$(15m+6m)v2
得:v=$\sqrt{\frac{5gL}{21}}$.
对木块从A滑至C过程,由于木块在AB段与桌面无摩擦,所以由能量守恒得:2mg×3L=15μmg×L
解得:μ=0.4
(2)设木块滑动距离x时停止,由能量守恒得:$\frac{x}{L}$mg(2L$+\frac{x}{2}$)=15μ1mg(x-L)
代入数据得:x=3L
另解x′=3.5L舍去,因为当x′=3.5L时,竖直悬挂部分绳的重力为5.5mg,木块所受的摩擦力为15μ1mg=5.25 mg<5.5mg,所以木块不可能停止运动.
答:(1)木块刚滑至B点时的速度为$\sqrt{\frac{5gL}{21}}$,动摩擦因数为0.4.
(2)木块最终停在3L处.
点评 让学生掌握机械能守恒定律及其成立条件,并理解功能关系.同时还运用假设法去分析与解决问题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
2.如图,水平地面上叠放着A和B,用一水平力F推物体B,A、B一起匀速运动,则( )


| A. | A、B之间的摩擦力一定为零 | B. | A、B之间的摩擦力方向向右 | ||
| C. | B和地面间的摩擦力一定不为零 | D. | B和地面间的摩擦力一定为零 |
12. 如图,电池组的内阻可以忽略不计,电压表和可变电阻器R串联接成电路,如果可变电阻器R的值减为原来的$\frac{1}{3}$,电压表的示数由U0增大到2U0,则下列说法正确的是( )
如图,电池组的内阻可以忽略不计,电压表和可变电阻器R串联接成电路,如果可变电阻器R的值减为原来的$\frac{1}{3}$,电压表的示数由U0增大到2U0,则下列说法正确的是( )
 如图,电池组的内阻可以忽略不计,电压表和可变电阻器R串联接成电路,如果可变电阻器R的值减为原来的$\frac{1}{3}$,电压表的示数由U0增大到2U0,则下列说法正确的是( )
如图,电池组的内阻可以忽略不计,电压表和可变电阻器R串联接成电路,如果可变电阻器R的值减为原来的$\frac{1}{3}$,电压表的示数由U0增大到2U0,则下列说法正确的是( )| A. | 流过可变电阻器R的电流增大到原来的2倍 | |
| B. | 可变电阻器R消耗的功率增大到原来的4倍 | |
| C. | 可变电阻器R两端的电压减小到原来的$\frac{2}{3}$ | |
| D. | 若可变电阻器R的阻值减小到零,那么电压表的示数变为4U0 |
19.关于磁感应强度的概念,以下说法中正确的有( )
| A. | 电流元IL在磁场中受力为F,则磁感应强度B一定等于$\frac{F}{IL}$ | |
| B. | 磁场中电流元受力大的地方,磁感应强度一定大 | |
| C. | 电流元IL在磁场中受力为F,则磁感应强度可能大于或等于$\frac{F}{IL}$ | |
| D. | 磁场中某点磁感应强度的方向,与电流元在此点的受力方向相同 |
16.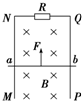 如图所示,竖直平行金属导轨MN、PQ上端接有电阻R,金属杆质量为m,跨在平行导轨上,垂直导轨平面的水平匀强磁场为B,不计ab与导轨电阻,不计摩擦,且ab与导轨接触良好.若ab杆在竖直向上的外力F作用下匀速上升,则以下说法正确的是( )
如图所示,竖直平行金属导轨MN、PQ上端接有电阻R,金属杆质量为m,跨在平行导轨上,垂直导轨平面的水平匀强磁场为B,不计ab与导轨电阻,不计摩擦,且ab与导轨接触良好.若ab杆在竖直向上的外力F作用下匀速上升,则以下说法正确的是( )
 如图所示,竖直平行金属导轨MN、PQ上端接有电阻R,金属杆质量为m,跨在平行导轨上,垂直导轨平面的水平匀强磁场为B,不计ab与导轨电阻,不计摩擦,且ab与导轨接触良好.若ab杆在竖直向上的外力F作用下匀速上升,则以下说法正确的是( )
如图所示,竖直平行金属导轨MN、PQ上端接有电阻R,金属杆质量为m,跨在平行导轨上,垂直导轨平面的水平匀强磁场为B,不计ab与导轨电阻,不计摩擦,且ab与导轨接触良好.若ab杆在竖直向上的外力F作用下匀速上升,则以下说法正确的是( )| A. | 拉力F所做的功等于电阻R上产生的热量 | |
| B. | 电流所做的功等于重力势能的增加量 | |
| C. | 杆ab克服安培力做的功等于电阻R上产生的热量 | |
| D. | 拉力F与重力做功的代数和等于电阻R上产生的热量 |
17.从青岛四方站开往济南的动车组D608次列车时刻表见表所示,则列车从潍坊到济南的平均速率是122.3km/h.
| 车站 | 到达时刻 | 开车时刻 | 行走时间/h | 路程/km | |
| 1 | 四方 | 16:56 | 16:56 | 0 | 0 |
| 2 | 潍坊 | 17:56 | 17:58 | 1 | 177 |
| 3 | 青州 | 18:20 | 18:21 | $1\frac{2}{5}$ | 234 |
| 4 | 淄博 | 18:42 | 18:44 | $1\frac{23}{30}$ | 277 |
| 5 | 济南 | 19:39 | 19:39 | $2\frac{43}{60}$ | 387 |
 中国首次太空授课活动于2013年6月20日上午10时许举行,神舟十号航天员在天宫一号开展基础物理实验,为全国青少年进行太空授课.其中女航天员王亚平利用“质量测量仪”在太空测出了指令长聂海胜的质量.
中国首次太空授课活动于2013年6月20日上午10时许举行,神舟十号航天员在天宫一号开展基础物理实验,为全国青少年进行太空授课.其中女航天员王亚平利用“质量测量仪”在太空测出了指令长聂海胜的质量.


