题目内容
如图，长为L=0.5m、质量为m=1.0kg的薄壁箱子，放在水平地面上，箱子与水平地面间的动摩擦因数μ=0.3．箱内有一质量也为m=1.0kg的小滑块，滑块与箱底间无摩擦．开始时箱子静止不动，小滑块以v=4m/s的恒定速度从箱子的A壁处向B壁处运动，之后与B壁碰撞．滑块与箱壁每次碰撞的时间极短，可忽略不计．滑块与箱壁每次碰撞过程中，系统的机械能没有损失．g=10m/s2．求：（1）要使滑块与箱子这一系统损耗的总动能不超过其初始动能的50%，滑块与箱壁最多可碰撞几次？
（2）从滑块开始运动到滑块与箱壁刚完成第三次碰撞的期间，箱子克服摩擦力做功的平均功率是多少？
（
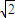=1.414，
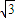=1.732，
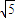=2.236，
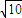3=.162）
【答案】分析：（1）根据题意可知，摩擦力做功导致系统的动能损失，从而即可求解；
（2）根据做功表达式，结合牛顿第二定律与运动学公式，从而可确定做功的平均功率．
解答：解：（1）设箱子相对地面滑行的距离为s，依动能定理和题目要求有系统损失的总动能为
×50%
解得
由于两物体质量相等，碰撞时无能量损失，故碰撞后交换速度．即小滑块与箱子碰后小滑块静止，箱子以小滑块的速度运动．如此反复．第一次碰后，小滑块静止，木箱前进L；第二次碰后，木箱静止，小滑块前进L；第三次碰后，小滑块静止，木箱前进L．因为L＜s＜2L，故二者最多碰撞3次．
（2）从滑块开始运动到刚完成第三次碰撞，箱子前进了L
箱子克服摩擦力做功W=2μmgL=3J
第一次碰前滑块在箱子上匀速运动的时间
第二次碰前箱子匀减速的加速度大小
设箱子匀减速的末速度为v，时间为t2
v2-v2=2aL
v=v+at2
求出t2=0.14s
第三次碰前滑块在箱子上匀速运动的时间t3=
从滑块开始运动到刚完成第三次碰撞经历的总时间为 t=t1+t2+t3=0.425s
摩擦力做功的平均功率为 P=
答：（1）要使滑块与箱子这一系统损耗的总动能不超过其初始动能的50%，滑块与箱壁最多可碰撞3次；
（2）从滑块开始运动到滑块与箱壁刚完成第三次碰撞的期间，箱子克服摩擦力做功的平均功率是7.1W．
点评：考查做功的求法，掌握动能定理的应用，学会由牛顿第二定律与运动学公式综合解题的方法，理解求平均功率与瞬时功率的区别．
（2）根据做功表达式，结合牛顿第二定律与运动学公式，从而可确定做功的平均功率．
解答：解：（1）设箱子相对地面滑行的距离为s，依动能定理和题目要求有系统损失的总动能为
×50%解得
由于两物体质量相等，碰撞时无能量损失，故碰撞后交换速度．即小滑块与箱子碰后小滑块静止，箱子以小滑块的速度运动．如此反复．第一次碰后，小滑块静止，木箱前进L；第二次碰后，木箱静止，小滑块前进L；第三次碰后，小滑块静止，木箱前进L．因为L＜s＜2L，故二者最多碰撞3次．
（2）从滑块开始运动到刚完成第三次碰撞，箱子前进了L
箱子克服摩擦力做功W=2μmgL=3J
第一次碰前滑块在箱子上匀速运动的时间
第二次碰前箱子匀减速的加速度大小
设箱子匀减速的末速度为v，时间为t2
v2-v2=2aL
v=v+at2
求出t2=0.14s
第三次碰前滑块在箱子上匀速运动的时间t3=
从滑块开始运动到刚完成第三次碰撞经历的总时间为 t=t1+t2+t3=0.425s
摩擦力做功的平均功率为 P=
答：（1）要使滑块与箱子这一系统损耗的总动能不超过其初始动能的50%，滑块与箱壁最多可碰撞3次；
（2）从滑块开始运动到滑块与箱壁刚完成第三次碰撞的期间，箱子克服摩擦力做功的平均功率是7.1W．
点评：考查做功的求法，掌握动能定理的应用，学会由牛顿第二定律与运动学公式综合解题的方法，理解求平均功率与瞬时功率的区别．
练习册系列答案
相关题目
动，R1=R2=1欧，导线ab和导轨的电阻不计，求磁场对导线ab的作用力。 
