题目内容
17.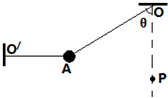 两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )
两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )| A. | 水平细线O′A剪断后的瞬间,OA细线拉力为$\frac{mg}{2}$ | |
| B. | 水平细线O′A剪断后的瞬间,小球A的加速度方向水平向右 | |
| C. | 细线碰到P后的瞬间,OA细线拉力为5mg | |
| D. | 细线碰到P后恰能作完整的圆周运动 |
分析 AB、水平细线O′A剪断后,小球将做圆周运动,则在剪断的瞬间,合力沿着垂直于绳子方向向下,沿着绳子方向受力平衡,对A球受力分析,根据沿着绳子方向合力为零列式求出此时绳子的拉力;
C、从剪断绳子到最低点的过程中,根据动能定理求出碰到P点时的速度,在最低点,根据向心力公式求解绳子的拉力;
D、若小球能做完整的圆周运动,则从最低点到最高点的过程中,根据动能定理求出到达最高点的速度,绳球模型中,小球恰好到达最高点时,绳子的拉力为零,重力提供向心力,求出最高点的最小速度,判断是否能做完整的圆周运动.
解答 解:A、水平细线O′A剪断后的瞬间,合力沿着垂直于绳子方向向下,即加速度方向沿着垂直于绳子方向向下,而沿着绳子方向受力平衡,对A球受力分析,受到OA绳子的拉力和重力作用,则有:T=mgcos60°=$\frac{1}{2}mg$,故A正确,B错误;
B、从剪断绳子到最低点的过程中,根据动能定理得:
$\frac{1}{2}m{v}^{2}=mgL(1-cos60°)$
解得:$v=\sqrt{gL}$
细线碰到P后的瞬间,线速度大小不变,根据向心力公式得:
T$′-mg=m\frac{{v}^{2}}{L-\frac{3}{4}L}$
解得:T′=5mg,故C正确;
D、若小球能做完整的圆周运动,则从最低点到最高点的过程中,根据动能定理得:
$\frac{1}{2}mv{′}^{2}-\frac{1}{2}m{v}^{2}=-mg•2•\frac{L}{4}$
解得:v′=0,
绳球模型中,小球恰好到达最高点时,绳子的拉力为零,重力提供向心力,则最高点有:
mg=m$\frac{v{″}^{2}}{\frac{L}{4}}$
解得:$v″=\frac{\sqrt{gL}}{2}$,所以小球不能做完整的圆周运动,故D错误.
故选:AC
点评 本题主要考查了向心力公式以及动能定理的直接应用,要求同学们能正确分析小球的受力情况和运动情况,知道细线碰到P点的瞬间线速度不变,还要清楚绳球模型中,小球恰好到达最高点时,绳子的拉力为零,重力提供向心力,难度适中.

| A. | 光速不变原理指出光在真空中传播速度在不同惯性参考系中都是相同的 | |
| B. | 变化的电场一定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| C. | 在光的双缝干涉实验中,若仅将入射光由红光改为绿光,则干涉条纹间距变宽 | |
| D. | 声源与观察者相对靠近时,观察者所接收的频率小于声源振动的频率 |
 趣味运动会上运动员手持网球拍托球沿水平面匀加速跑,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
趣味运动会上运动员手持网球拍托球沿水平面匀加速跑,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )| A. | 运动员的加速度为gtanθ | |
| B. | 球拍对球的作用力为$\frac{mg}{sinθ}$ | |
| C. | 运动员对球拍的作用力为$\frac{Mg}{cosθ}$ | |
| D. | 若加速度大于gsinθ,球一定沿球拍向上运动 |
 图甲是电场中一条电场线,A,B是电场线上的两点,一带正电粒子(只受电场力)沿直线从A点运动到B点的v-t图象如图乙所示,则关于A,B两点的电场强度EA和EB的下列说法正确的是( )
图甲是电场中一条电场线,A,B是电场线上的两点,一带正电粒子(只受电场力)沿直线从A点运动到B点的v-t图象如图乙所示,则关于A,B两点的电场强度EA和EB的下列说法正确的是( )| A. | 该电场一定是匀强电场 | |
| B. | EA<EB,电场方向从A向B | |
| C. | EA>EB,电场方向从A向B | |
| D. | 若该电场是由点电荷产生,在点电荷一定在B点的右方 |
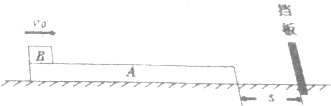
 如图所示,一个质量为M木箱原来静止在光滑水平面上,木箱内粗糙的底板上放着一个质量为m的小木块,m=0.25M,现使木箱获得一个向右的初速度v0,则( )
如图所示,一个质量为M木箱原来静止在光滑水平面上,木箱内粗糙的底板上放着一个质量为m的小木块,m=0.25M,现使木箱获得一个向右的初速度v0,则( )| A. | 木箱运动和小木块最终都静止 | |
| B. | 小木块最终速度大小为4v0,方向向右 | |
| C. | 木箱最终速度大小为0.8v0,方向向右 | |
| D. | 如果小木块与木箱的左壁碰撞后相对木箱静止,则二者将一起向左运动 |
| A. | 甲大 | B. | 乙大 | C. | 一样大 | D. | 都有可能 |
 如图所示,光滑水平面上有一平板车,车上固定一竖直直杆,杆的最高点O通过一长为L的轻绳拴接一个可视为质点的小球,小球的质量为小车(包括杆的质量)质量的一半,悬点O距离地面的高度为2L,轻绳水平时,小球与小车速度均为零.释放小球,当小球运动到最低点时.求:(重力加速度为g)
如图所示,光滑水平面上有一平板车,车上固定一竖直直杆,杆的最高点O通过一长为L的轻绳拴接一个可视为质点的小球,小球的质量为小车(包括杆的质量)质量的一半,悬点O距离地面的高度为2L,轻绳水平时,小球与小车速度均为零.释放小球,当小球运动到最低点时.求:(重力加速度为g)