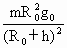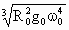题目内容
用m表示地球的同步卫星的质量,h表示它离地面的高度,R0表示地球的半径,g0表示地球表面的重力加速度,ω0为地球自转的角速度,则该卫星所受地球的万有引力为F,则( )
分析:由题地球的同步卫星的轨道半径为R=R0+h.根据地球的半径和地球表面的重力加速度,由重力等于万有引力,可求出地球的质量.地球的同步卫星的角速度与地球的自转的角速度相同,轨道平面必须与赤道平面重合.由向心力公式求解向心力.
解答:解:A、该卫星所受地球的万有引力为F=G
=G
,由于地球的质量M和卫星的质量m均不是已知量,故A错误.
B、由mg0=
,得到GM=g0R02,代入A项中得到F=
.故B正确.
C、地球的同步卫星的角速度与地球的自转的角速度ω0相同,轨道半径为R=R0+h,则F=mω02(R0+h).故C正确.
D、地球的同步卫星的必要条件是:轨道平面必须与赤道平面重合,否则卫星在其他平面运动时,由于地球的万有引力,卫星不能保持稳定.故D正确.
故选BCD
| Mm |
| R2 |
| Mm |
| (R0+h)2 |
B、由mg0=
| GMm | ||
|
mg0
| ||
| (R0+h)2 |
C、地球的同步卫星的角速度与地球的自转的角速度ω0相同,轨道半径为R=R0+h,则F=mω02(R0+h).故C正确.
D、地球的同步卫星的必要条件是:轨道平面必须与赤道平面重合,否则卫星在其他平面运动时,由于地球的万有引力,卫星不能保持稳定.故D正确.
故选BCD
点评:对于地球同步卫星的必要条件有两个:一是轨道平面必须与赤道平面重合;二是角速度与地球的自转的角速度ω0相同.

练习册系列答案
相关题目
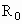 表示地球的半径,
表示地球的半径,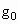 表示地球表面处的重力加速度,
表示地球表面处的重力加速度,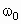 表示地球自转的角速度.则通讯卫星所受的地球万有引力的大小为
表示地球自转的角速度.则通讯卫星所受的地球万有引力的大小为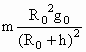
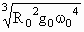 (4)以上结果都不正确
(4)以上结果都不正确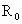 表示地球的半径,
表示地球的半径,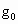 表示地球表面处的重力加速度,
表示地球表面处的重力加速度,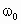 表示地球自转角速度,则通讯卫星所受地球对它的万有引力的大小
表示地球自转角速度,则通讯卫星所受地球对它的万有引力的大小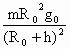
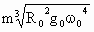
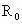 表示地球的半径,
表示地球的半径,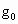 表示地球表面处的重力加速度,
表示地球表面处的重力加速度,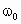 表示地球自转角速度,则通讯卫星所受地球对它的万有引力的大小为
表示地球自转角速度,则通讯卫星所受地球对它的万有引力的大小为