题目内容
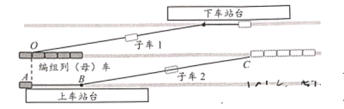
【题目】如图甲，轻弹簧一端固定在地面上，在弹簧上端轻轻放上质量为M的物块，物块的振幅为A。现把该轻弹簧放在光滑水平轨道上，左端固定，右端连接质量为
的竖直挡板，处于原长时挡板位于轨道上的B点。水平轨道的右侧与倾角为37°的斜面在D点平滑连接，斜面与圆轨道相切于E点，斜面长度x和圆轨道的半径R相等，
A，OF、OG分别是圆轨道的水平半径和竖直半径，B、C、D、E、F、G均在同一竖在面内，斜面和圆弧轨道均是粗糙的。用物块M通过挡板压缩弹簧到C点，使BC=2A，从静止释放，M与挡板分离后冲上斜面，恰好能运动到G点。物块在圆弧上EF、FG两段上克服摩擦力做的功相等，在F点时对轨道的压力
=3.2Mg，已知sin37°=0.6，co37°=0.8，重力加速度为g，求：
（1）甲图中弹簧的最大弹性势能；
（2）物块与挡板脱离时的速度大小；
（3）物块在圆弧FG段上克服摩擦力做的功；
（4）物块与斜面之间的动摩擦因数。
【答案】（1）
；（2）
；（3）
；（4）
【解析】
（1）在弹簧上端轻轻放上质量为M的物块，由对称性知，到最低点时有
k(2A) -Mg=Mg ①
弹簧的劲度系数k=
，弹簧的最大弹性势能
②
（2）物块与挡板在B点脱离，由能量守恒
k(2A)2=（M+
M）v2 ③
由②③物块与挡板脱离时的速度大小v=
（3）在F点由牛顿第二定律得
④
恰好能运动到G点，在G点由牛顿第二定律得：
⑤
从F点到G点由动能定理得
⑥
由④⑤⑥解得物块在圆弧FG段上克服摩擦力做的功
（4）物块与挡板脱离后运动到F点，由动能定理得：
⑦
由④⑥⑦解得物块与斜面之间的动摩擦因数。
答：（1）弹簧的最大弹性势能为；（2）物块与挡板脱离时的速度大小为；（3）物块在圆弧FG段上克服摩擦力做的功为；（4）物块与斜面之间的动摩擦因数。
