Question

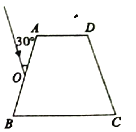
【题目】如图所示，某种透明材料制成的等腰梯形玻璃砖，截面如图所示，其中底边BC长为，∠B=75°，O点在AB边上，与B点距离为10cm，现有一束单色光于AB边从O点与AB边成30°角射入玻璃砖，已知单色光在玻璃砖中的折射率为，在真空中的传播速度为，（，结果可用根号表示）。求：

（i）单色光从玻璃砖中射出的折射角；

（ii）单色光在玻璃砖中的传播时间；

Answer 1

【答案】（i）r=60（ii）

【解析】（ⅰ）作出光路图如图所示，单色光在AB界面的入射角i=60；

设折射角为α，由折射定律，

由，可得α=30，

由几何关系知单色光在BC界面的入射角θ=∠B－α＝45，

设单色光临界角分别为，由，有，

可知，单色光在BC界面发生全反射，单色光AC界面的入射角为β，可知β＝α=30，

设折射角为r，，可知r=60；

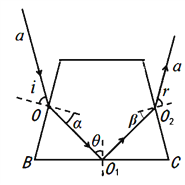
（ⅱ）在中∠B=75，由正弦定理知，；

可得，，

则，可知与全等，

可得，

单色光在玻璃砖中的总路程；

由可知单色光在玻璃砖中的传播速度，

单色光在玻璃砖中的传播时间；