Question

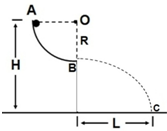如图所示，位于竖直平面上半径为R=0.8m的1/4圆弧光滑轨道AB，A点距离地面高度为H=1m，质量为m=0.1kg的小球从A点由静止释放，通过1/4圆弧光滑轨道AB，最后落在距B点水平距离为L=4m的地面C处，不计空气阻力，g=10m/s²求：
（1）小球通过B点的速度；
（2）小球通过B点时对B点的压力．

Answer 1

分析：（1）根据动能定理小球通过B点的速度．
（2）根据牛顿第二定律求出小球通过B点时支持力的大小，从而得出小球对B点的压力大小．

解答：解：（1）由A→B过程，由动能定理，有：
 mgR=

1

2

mv_B²                  
解得：
vB=

2gR

=

2×10×0.8

=4m/s；
（2）小球沿圆弧做圆周运动，在B点，由牛顿第二定律，有：
F_N-mg=m

v 2 B

R

            
解得：F_N=3mg=3×0.1×10=3N
根据牛顿第三定律，小球对B点的压力为3N；
答：（1）小球通过B点的速度为4m/s；
（2）小球通过B点时对B点的压力为3N．

点评：本题关键是明确小球做圆周运动过程中，只有重力做功，根据动能定理列式求解B点速度，根据牛顿第二定律求解B点的弹力，基础题．