题目内容
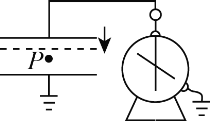
【题目】如图所示，带正电的粒子以一定的初速度
沿两板的中线进入水平放置的已经充满电的平行板电容器内，仅在电场力的作用下，恰好沿下板的边缘飞出，已知平行板间距离为
，板间电压为
，带电粒子的电荷量为
，粒子通过平行板的时间为
，则
A. 在后
时间内，电场力对粒子做的功为
B. 粒子在竖直方向下落前
和后
的过程中，电场力做功之比为1∶2
C. 在整个
时间内，电场力对粒子做功为
D. 在前
和后
时间内，粒子的动能增量之比为1：3
【答案】D
【解析】试题分析，粒子在电场中做类平抛运动，在竖直方向上做初速度为零的匀加速直线运动，根据运动学规律求解在前
与后
时间内竖直方向上的位移比，然后结合
，计算电场力对粒子做的功，因为粒子只受电场力，所以根据动能定理求解粒子动能的增量；根据
计算在前下落前
和后
的过程中电场力做的功；根据
计算粒子整个过程中电场力做的功。
带电粒子在竖直方向上做初速度为零的匀加速直线运动，故在前
与后
时间内竖直方向上的位移之比为
，因为
，所以
，又因为在匀强电场中，电势沿电场线方向均匀降低，故在前
时间内电场力做功为
，在后
时间内电场力做功为
，根据动能定理可得
， 
， 
，故A错误D正确；粒子在竖直方向下落前
和后
的过程中，根据
可得做功分别为
、
，故做功之比为1:1，B错误；在整个
时间内，电场力对粒子做功为
，C错误；
练习册系列答案
相关题目
