题目内容
如图所示,在平面直角坐标系XOY内,第I象限存在沿Y轴正方向的匀强电场,第IV象限内存在垂直于坐标平面向里的匀强磁场,磁感应强度大小设为B1(未知),第III象限内也存在垂直于坐标平面向里的匀强磁场B2(未知).一质量为m的电子(电量为e,不计重力),从Y轴正半轴上Y=h处的M点,以速度v0垂直于Y轴射入电场,经X轴上X=
h处的P点进入第IV象限磁场,然后从Y轴上Q点进入第III象限磁场,OQ=OP,最后从O点又进入电场.
(1)求匀强电场的场强大小E;
(2)求粒子经过Q点时速度大小和方向;
(3)求B1与B2之比为多少.
2
| ||
| 3 |
(1)求匀强电场的场强大小E;
(2)求粒子经过Q点时速度大小和方向;
(3)求B1与B2之比为多少.

(1)电子在电场中做类平抛运动,则
x=v0t=
h
h=
at2
又由牛顿第二定律得 a=
解得:E=
(2)画出电子在磁场中运动的轨迹图,

vy=at=
v0
∴v=
=2v0
tanθ=
=
∴θ=60
∴∠OPO1=30° 又∵OQ=OP
由几何关系得∠OQO1=∠OPO1=30°
∴粒子到达Q点时速度方向与y轴正向成60°
(3)由几何关系得 r1cos30°+r1sin30°=op=
h
∴r1=(2-
)h
又r1=
=
进入B2后,
由几何关系得:2r2cos30°=OQ=OP=
h
∴r2=
h
又r2=
∴
=
=
答:
(1)匀强电场的场强大小E是
;
(2)粒子经过Q点时速度大小为2v0,方向与y轴正向成60°;
(3)B1与B2之比为
.
x=v0t=
| 2 |
| 3 |
| 3 |
h=
| 1 |
| 2 |
又由牛顿第二定律得 a=
| eE |
| m |
解得:E=
| 3mv02 |
| 2eh |
(2)画出电子在磁场中运动的轨迹图,

vy=at=
| 3 |
∴v=
|
tanθ=
| vy |
| v0 |
| 3 |
∴θ=60
∴∠OPO1=30° 又∵OQ=OP
由几何关系得∠OQO1=∠OPO1=30°
∴粒子到达Q点时速度方向与y轴正向成60°
(3)由几何关系得 r1cos30°+r1sin30°=op=
| 2 |
| 3 |
| 3 |
∴r1=(2-
| 2 |
| 3 |
| 3 |
又r1=
| mv |
| eB1 |
| 2mv0 |
| eB1 |
由几何关系得:2r2cos30°=OQ=OP=
| 2 |
| 3 |
| 3 |
∴r2=
| 2 |
| 3 |
又r2=
| 2mv0 |
| eB2 |
| B1 |
| B2 |
| r2 |
| r1 |
3+
| ||
| 6 |
答:
(1)匀强电场的场强大小E是
3m
| ||
| 2eh |
(2)粒子经过Q点时速度大小为2v0,方向与y轴正向成60°;
(3)B1与B2之比为
3+
| ||
| 6 |

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 如图所示,在平面直角坐标系xOy的第一象限内,有垂直纸面向里的匀强磁场,磁感应强度为B=2T.一对电子和正电子从O点沿纸面以相同的速度v射入磁场中,速度方向与磁场边界0x成30.角,求:电子和止电子在磁场中运动的时间为多少?
如图所示,在平面直角坐标系xOy的第一象限内,有垂直纸面向里的匀强磁场,磁感应强度为B=2T.一对电子和正电子从O点沿纸面以相同的速度v射入磁场中,速度方向与磁场边界0x成30.角,求:电子和止电子在磁场中运动的时间为多少? 如图所示,在平面直角坐标系xOy的第II、III象限内存在沿y轴负方向的匀强电场,场强E=50V/m;一圆心在O1点,半径R=5cm的绝缘弹性圆筒在与y轴切点O处开有小孔a,筒内有垂直纸面向里的匀强磁场.现从P(-10cm,-5cm)处沿与x轴正向成45°方向发射比荷q/m=2×103C/kg的带正电粒子,粒子都恰能通过原点O沿x轴正向射出电场并进入磁场.不计粒子重力,试求:
如图所示,在平面直角坐标系xOy的第II、III象限内存在沿y轴负方向的匀强电场,场强E=50V/m;一圆心在O1点,半径R=5cm的绝缘弹性圆筒在与y轴切点O处开有小孔a,筒内有垂直纸面向里的匀强磁场.现从P(-10cm,-5cm)处沿与x轴正向成45°方向发射比荷q/m=2×103C/kg的带正电粒子,粒子都恰能通过原点O沿x轴正向射出电场并进入磁场.不计粒子重力,试求: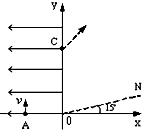 如图所示,在平面直角坐标系xoy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿Y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求:
如图所示,在平面直角坐标系xoy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿Y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求: 如图所示,在平面直角坐标系xoy的0≤x≤2L、0≤y≤L区域内存在沿y轴正向的匀强电场,一质量为m,电荷量为q,不计重力,带正电的粒子以速度v0从坐标原点O沿x轴正向射入电场后,恰好从M(2L,L)点离开电场,粒子离开电场后将有机会进入一个磁感应强度大小为
如图所示,在平面直角坐标系xoy的0≤x≤2L、0≤y≤L区域内存在沿y轴正向的匀强电场,一质量为m,电荷量为q,不计重力,带正电的粒子以速度v0从坐标原点O沿x轴正向射入电场后,恰好从M(2L,L)点离开电场,粒子离开电场后将有机会进入一个磁感应强度大小为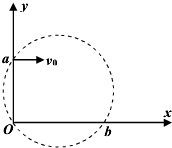 如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )
如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )