题目内容
如图甲所示,质量为m=0.5kg、电阻r=1Ω的跨接杆ab可以无摩擦地沿水平固定导轨滑行,导轨足够长,两导轨间宽度为L=1m,导轨电阻不计,电阻R1=1.5Ω,R2=3Ω,装置处于竖直向下的匀强磁场中,磁感应强度为B=1T.杆从x轴原点O以水平初速度向右滑行,直到停止.已知杆在整个运动过程中v随位移x变化的关系如图乙所示.求:
(1)在杆的整个运动过程中,电流对电阻R1做的功,
(2)在杆的整个运动过程中,通过电阻R1的电量,
(3)要使R1产生1J的热量,杆需向右移动的距离及此时R1的功率.
(1)在杆的整个运动过程中,电流对电阻R1做的功,
(2)在杆的整个运动过程中,通过电阻R1的电量,
(3)要使R1产生1J的热量,杆需向右移动的距离及此时R1的功率.

(1)设整个电路中电流做功为W,则根据功能关系得
W=
m
=
×0.5×42J=4J
设杆中瞬时电流为I,则电流对杆做功Wab=I2rt,
电流对R1做功W1=I12R1t,电流对R2做功W2=I22R2t,
由于
=
=2,则I1=
I,I2=
I
又r=1Ω,R1=1.5Ω,R2=3Ω,得Wab=1.5W1,W2=0.5W1,
∵W=Wab+W1+W2=3W1,
∴W1=
W=
J
(2)根据
=
,
=
,q=
?△t,△Φ=BLx
联立得,通过杆的电量q=
代入解得,q=2C
由于R1与R2并联,电流与电阻成反比,而电量q=It,则得
通过电阻R1的电量q1=
q=
C
(3)要使R1产生1J的热量,由上题电功关系可知,R1产生0.5J的热量,杆产生的热量为1.5J,电路中产生的总热量为Q=1J+0.5J+1.5J=3J
设此时杆的速度为v,由能量守恒得
Q+
mv2=
m
,
解得v=2m/s
由图知,杆需向右移动的距离x=1m
此时杆产生的感应电动势为E=BLv=2V,干路中电流为I=
=1A
则I1=
I=
A
此时R1的功率为P=
R1=
W
答:
(1)在杆的整个运动过程中,电流对电阻R1做的功为
J,
(2)在杆的整个运动过程中,通过电阻R1的电量为
C,
(3)要使R1产生1J的热量,杆需向右移动的距离为2m,此时R1的功率为
W.
W=
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
设杆中瞬时电流为I,则电流对杆做功Wab=I2rt,
电流对R1做功W1=I12R1t,电流对R2做功W2=I22R2t,
由于
| I1 |
| I2 |
| R2 |
| R1 |
| 2 |
| 3 |
| 1 |
| 3 |
又r=1Ω,R1=1.5Ω,R2=3Ω,得Wab=1.5W1,W2=0.5W1,
∵W=Wab+W1+W2=3W1,
∴W1=
| 1 |
| 3 |
| 4 |
| 3 |
(2)根据
| . |
| E |
| △Φ |
| △t |
| . |
| I |
| ||
r+
|
| . |
| I |
联立得,通过杆的电量q=
| BLx | ||
r+
|
代入解得,q=2C
由于R1与R2并联,电流与电阻成反比,而电量q=It,则得
通过电阻R1的电量q1=
| R2 |
| R1+R2 |
| 4 |
| 3 |
(3)要使R1产生1J的热量,由上题电功关系可知,R1产生0.5J的热量,杆产生的热量为1.5J,电路中产生的总热量为Q=1J+0.5J+1.5J=3J
设此时杆的速度为v,由能量守恒得
Q+
| 1 |
| 2 |
| 1 |
| 2 |
| v | 20 |
解得v=2m/s
由图知,杆需向右移动的距离x=1m
此时杆产生的感应电动势为E=BLv=2V,干路中电流为I=
| E |
| R |
则I1=
| 2 |
| 3 |
| 2 |
| 3 |
此时R1的功率为P=
| I | 21 |
| 2 |
| 3 |
答:
(1)在杆的整个运动过程中,电流对电阻R1做的功为
| 4 |
| 3 |
(2)在杆的整个运动过程中,通过电阻R1的电量为
| 4 |
| 3 |
(3)要使R1产生1J的热量,杆需向右移动的距离为2m,此时R1的功率为
| 2 |
| 3 |

练习册系列答案
相关题目
 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施加平行于斜面向上的恒力F,作用时间t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示,取g=10m/s2.试求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施加平行于斜面向上的恒力F,作用时间t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示,取g=10m/s2.试求: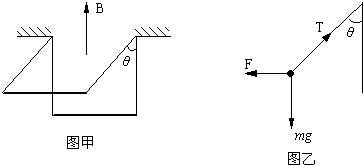
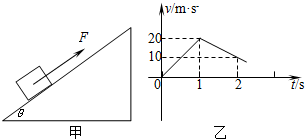 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.试求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.试求: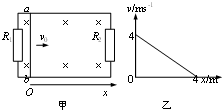 如图甲所示,质量为m=0.5kg、电阻r=1Ω的跨接杆ab可以无摩擦地沿水平固定导轨滑行,导轨足够长,两导轨间宽度为L=1m,导轨电阻不计,电阻R1=1.5Ω,R2=3Ω,装置处于竖直向下的匀强磁场中,磁感应强度为B=1T.杆从x轴原点O以水平初速度向右滑行,直到停止.已知杆在整个运动过程中v随位移x变化的关系如图乙所示.求:
如图甲所示,质量为m=0.5kg、电阻r=1Ω的跨接杆ab可以无摩擦地沿水平固定导轨滑行,导轨足够长,两导轨间宽度为L=1m,导轨电阻不计,电阻R1=1.5Ω,R2=3Ω,装置处于竖直向下的匀强磁场中,磁感应强度为B=1T.杆从x轴原点O以水平初速度向右滑行,直到停止.已知杆在整个运动过程中v随位移x变化的关系如图乙所示.求: