题目内容
19. 如图所示,在正交坐标系Oxyz中,分布着电场和磁场(图中未画出).在Oyz平面的左方空间内存在沿y轴负方向、磁感应强度大小为B的匀强磁场;在Oyz平面右方、Oxz平面上方的空间内分布着沿z轴负方向、磁感应强度大小也为B匀强磁场;在Oyz平面右方、Oxz平面下方分布着沿y轴正方向的匀强电场.在t=0时刻,一个微粒的质量为m、电荷量为q的微粒从P点静止释放,已知P点的坐标为(5a,-2a,0),电场强度大小为$\frac{aq{B}^{2}}{4m}$,不计微粒的重力.
如图所示,在正交坐标系Oxyz中,分布着电场和磁场(图中未画出).在Oyz平面的左方空间内存在沿y轴负方向、磁感应强度大小为B的匀强磁场;在Oyz平面右方、Oxz平面上方的空间内分布着沿z轴负方向、磁感应强度大小也为B匀强磁场;在Oyz平面右方、Oxz平面下方分布着沿y轴正方向的匀强电场.在t=0时刻,一个微粒的质量为m、电荷量为q的微粒从P点静止释放,已知P点的坐标为(5a,-2a,0),电场强度大小为$\frac{aq{B}^{2}}{4m}$,不计微粒的重力.求:
(1)微粒第一次到达x轴的速度大小v和时刻t1;
(2)微粒第一次到达y轴的坐标和时刻t2;
(3)假设在平面Oyz存在一层特殊物质,使微粒每次经过Oyz平面时,速度大小总变为原来的$\frac{1}{2}$,求在时刻t3=t2+$\frac{4πm}{qB}$时,电荷所在位置的坐标.
分析 (1)在电场中微粒做匀加速直线运动,根据动能定理求出微粒第一次到达x轴的速度大小v,由位移时间公式求解运动的时间.
(2)画出粒子微粒运动的轨迹.根据洛伦兹力充当向心力,列式求出轨迹半径,由几何关系求微粒第一次到达y轴的坐标.由周期求时间.
(3)粒子运动过程中速度始终与所在位置的磁场垂直,粒子刚好在oyz平面左右空间各运动半个周期后交替运动,粒子速度改变后在磁场中运动的周期不变,根据分析可知,微粒在oyz平面左方运动的轨迹为两个半圆和四分之一圆,在oyz平面右方运动的轨迹为两个半圆,分别穿过oyz平面5次.由几何知识求电荷的坐标.
解答 解:(1)在电场中微粒做匀加速直线运动,由题意E=$\frac{aq{B}^{2}}{4m}$
由动能定理得:qE•2a=$\frac{1}{2}m{v}^{2}$
解得:v=$\frac{aqB}{m}$
由$\frac{1}{2}•\frac{qE}{m}$${t}_{1}^{2}$=2a
得:t1=$\frac{4m}{qB}$
(2)当微粒在磁场中运动时,轨迹如下图所示.假设运动的轨道半径为R,
有:qvB=m$\frac{{v}^{2}}{R}$
可得 R=a
所以微粒到达y轴的坐标为(0,a,0).
磁场运动的周期 T=$\frac{2πR}{v}$=$\frac{2πm}{qB}$
则运动到达y轴的时刻 t2=5t1+$\frac{5}{4}T$
解得:t2=$(\frac{40+5π}{2})$$\frac{m}{qB}$
(3)粒子运动过程中速度始终与所在位置的磁场垂直,粒子刚好在oyz平面左右空间各运动半个周期后交替运动,因为:t3-t2=$\frac{9}{4}$T
且粒子速度改变后在磁场中运动的周期不变,根据分析可知,微粒在oyz平面左方运动的轨迹为两个半圆和四分之一圆,在oyz平面右方运动的轨迹为两个半圆.分别穿过oyz平面5次.所以:
x轴坐标为:x=-$(\frac{1}{2})^{5}$a=-$\frac{1}{32}$a
y轴坐标为:y=a+$(\frac{1}{2})^{2}$a×2+$(\frac{1}{2})^{4}$a×2=$\frac{13}{8}$a
z轴坐标为:z=$(\frac{1}{2})$a×2+$(\frac{1}{2})^{3}$a×2+$(\frac{1}{2})^{5}$a=$\frac{41}{32}$a
因此t3时刻的坐标为(-$\frac{1}{32}$a,$\frac{13}{8}$a,$\frac{41}{32}$a).
答:
(1)微粒第一次到达x轴的速度大小v为$\frac{aqB}{m}$,时刻t1为$\frac{4m}{qB}$.
(2)微粒第一次到达y轴的坐标为(0,a,0),时刻t2为$(\frac{40+5π}{2})$$\frac{m}{qB}$.
(3)在时刻t3=t2+$\frac{4πm}{qB}$时,电荷所在位置的坐标为(-$\frac{1}{32}$a,$\frac{13}{8}$a,$\frac{41}{32}$a).
点评 本题考查了粒子在电磁场、在电场中的运动,关键要分析清楚粒子运动过程,画出粒子的运动轨迹,要有空间想象能力,并能应用动能定理、牛顿第二定律、运动学公式等力学规律解答.

 如图所示,三条虚线表示某电场中的三个等势面,其电势分别为φ1=10V,φ2=20V,φ3=30V.图中实线AB是一个带电粒子只受电场力作用下运动的轨迹则( )
如图所示,三条虚线表示某电场中的三个等势面,其电势分别为φ1=10V,φ2=20V,φ3=30V.图中实线AB是一个带电粒子只受电场力作用下运动的轨迹则( )| A. | 粒子带负电,且一定是从A运动到B | |
| B. | 粒子在A点的速度大于在B点的速度 | |
| C. | 粒子在A点的加速度大于在B点的加速度 | |
| D. | 粒子在A点的电势能大于在B点的电势能 |
 如图甲为一台小型发电机构造图,线圈逆时针转动,产生的电动势随时间按余弦规律变化,其e-t图象如图乙所示.发电机线圈的内阻为1Ω,外接灯泡的电阻为9Ω,则( )
如图甲为一台小型发电机构造图,线圈逆时针转动,产生的电动势随时间按余弦规律变化,其e-t图象如图乙所示.发电机线圈的内阻为1Ω,外接灯泡的电阻为9Ω,则( )| A. | 电压表的示数为6V | |
| B. | 发电机的输出功率为4W | |
| C. | 在1.0×10-2s时刻,穿过线圈的磁通量最小 | |
| D. | 在2.0×10-2s时刻,穿过线圈的磁通量变化率最大 |
| A. | F1是由于书的弹性形变而产生的 | B. | F1与F2是一对相互作用力 | ||
| C. | F1与F2是一对平衡力 | D. | F2是由于桌面的弹性形变而产生的 |
 三个点电荷A,B,C固定在正方形的三个顶点,如图所示,点电荷A带电量为+2q,B,C带电量均为-q,下列判断正确的是( )
三个点电荷A,B,C固定在正方形的三个顶点,如图所示,点电荷A带电量为+2q,B,C带电量均为-q,下列判断正确的是( )| A. | 将点电荷A移动到无穷远,电场力对其做负功 | |
| B. | 将点电荷B移动到无穷远,电场力对其做正功 | |
| C. | 在D点放置合适的点电荷,释放点电荷A,A可能处于状态静止 | |
| D. | 在D点放置合适的点电荷,释放点电荷B.B可能处于静止状态 |
| A. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能增加 | |
| B. | 气体如果失去了容器的约束就会散开,这是因为气体分子之间存在势能的缘故 | |
| C. | 如果气体温度升高,那么所有分子的速率都增加 | |
| D. | 如果气体分子总数不变,而气体温度升高,气体分子的平均动能增大,因此压强必然增大 | |
| E. | 对于一定质量的气体,如果压强不变,体积增大,那么它一定从外界吸热 | |
| F. | 一定量气体的内能不等于其所有分子热运动动能和分子之间势能的总和 |
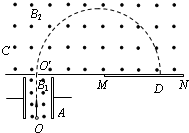 质谱仪是一种能够把具有不同荷质比(带电粒子的电荷和质量之比)的带电粒子分离开来的仪器,它的工作原理如图所示.其中A部分为粒子速度选择器,C部分是偏转分离器.如果速度选择器的两极板间匀强电场的电场强度为E,匀强磁场的磁感强度为B1.偏转分离器区域匀强磁场的磁感强度为B2,某种带电粒子由O点沿直线穿过速度选择器区域后进入偏转分离器.求:
质谱仪是一种能够把具有不同荷质比(带电粒子的电荷和质量之比)的带电粒子分离开来的仪器,它的工作原理如图所示.其中A部分为粒子速度选择器,C部分是偏转分离器.如果速度选择器的两极板间匀强电场的电场强度为E,匀强磁场的磁感强度为B1.偏转分离器区域匀强磁场的磁感强度为B2,某种带电粒子由O点沿直线穿过速度选择器区域后进入偏转分离器.求: