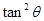题目内容
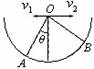
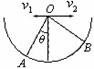
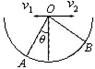
 如图所示,半圆形容器竖直放置,在其圆心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成θ角,则两小球的初速度之比为( )
如图所示,半圆形容器竖直放置,在其圆心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成θ角,则两小球的初速度之比为( )分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据平抛运动水平位移和竖直位移的关系确定两小球初速度大小之比.
解答:解:对于小球1,根据Rcosθ=
gt12,解得t1=
,则v1=
=Rsinθ
.
对于小球2,根据Rsinθ=
gt22,解得t2=
,则v2=
=Rcosθ
.
则两小球的初速度之比
=
.故C正确,A、B、D错误.
故选:C.
| 1 |
| 2 |
|
| Rsinθ |
| t1 |
|
对于小球2,根据Rsinθ=
| 1 |
| 2 |
|
| Rcosθ |
| t2 |
|
则两小球的初速度之比
| v1 |
| v2 |
| tan3θ |
故选:C.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
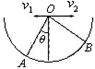
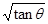
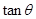
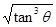
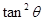
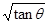 B.
B.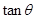
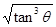 D.
D.