Question

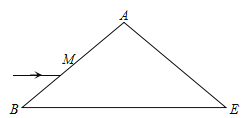
【题目】如图所示，棱镜的折射率为，其截面为等腰三角形。已知，BM=L，．在此截面所在的平面内，一条光线平行于BE边从AB边上的M点射入棱镜，最后从AE边上的N点平行于BE边射出（图中未画出）。真空中光速为c，不考虑光线在AB、AE边反射情况。sin37°=cos53°=0.6；cos37°=sin53°=0.8；sin74°=cos16°=0.96；cos74°=sin16°=0.28。

（ⅰ）求E、N两点间距离；

（ⅱ）求光在棱镜中传播的时间t。

Answer 1

【答案】（ⅰ）（ⅱ）

【解析】

光路图如图所示：

（ⅰ）在AB边上的M点：入射角为i＝53°，折射角为

由折射定律得：

解得：＝37°

在BE边上的D点：入射角θ＝74°

设全反射的临界角为C，则：sinC==0.75＜sin74°

因θ＞C，光在D点发生全反射。

在三角形MBD中，由正弦定理得：

解得：

由三角形MBD与三角形NED相似，则有：

（ⅱ）光在在棱镜中传播的速度：

时间：