题目内容
 做匀变速直线运动的小车,牵引一条纸带通过打点计时器,交流电源的频率是50Hz,由纸带上打出的某一点开始,每5点剪下一段纸带,按如图所示,每一条纸带下端与x轴相重合,在左边与y轴平行,将纸带粘在坐标系中,求:
做匀变速直线运动的小车,牵引一条纸带通过打点计时器,交流电源的频率是50Hz,由纸带上打出的某一点开始,每5点剪下一段纸带,按如图所示,每一条纸带下端与x轴相重合,在左边与y轴平行,将纸带粘在坐标系中,求:(1)第一个0.1s内中间时刻的瞬时速度是
(2)第一个0.1s的初速度是
(3)物体运动的加速度是
分析:(1)通过第一段时间内的位移求出平均速度,匀加速直线运动某段时间内的平均速度等于中间时刻的瞬时速度,据此可求出某点的瞬时速度.
(2)根据匀变速直线运动推论公式
=
,可以求出开始时刻小车速度大小,利用平均数速度等于位移除以时间求出0.6s内的平均速度.
(3)根据△x=aT2求出小车的加速度,然后根据速度时间公式求出坐标原点处的速度.
(2)根据匀变速直线运动推论公式
. |
| v |
| v0+v1 |
| 2 |
(3)根据△x=aT2求出小车的加速度,然后根据速度时间公式求出坐标原点处的速度.
解答:解:(1)根据匀变速直线运动中时间中点的瞬时速度等于某点的瞬时速度,有:
第一个0.1s内中间时刻的瞬时速度等于第一个0.1s内的平均速度:
v1=v=
=
=0.225m/s
第一个0.1s末速度为:
v2=
=
≈0.263m/s
(2)根据匀变速直线运动推论公式
=
得:
v1=
,因此有:
v0=2v1-v2=(2×0.225-0.263)m/s=0.187m/s
0.6s内的平均速度是:
=
═
=0.413m/s
(3)根据题意可知:△x=7.5mm,根据△x=aT2得:
a=
=
=0.75m/s2
故答案为:(1)0.225,0.263;(2)0.187,0.413;(3)0.75.
第一个0.1s内中间时刻的瞬时速度等于第一个0.1s内的平均速度:
v1=v=
| x1 |
| T |
| 22.5×10-3m |
| 0.1s |
第一个0.1s末速度为:
v2=
| x1+x2 |
| 2T |
| (22.5+30)×10-2m |
| 2×0.1s |
(2)根据匀变速直线运动推论公式
. |
| v |
| v0+v1 |
| 2 |
v1=
| v0+v2 |
| 2 |
v0=2v1-v2=(2×0.225-0.263)m/s=0.187m/s
0.6s内的平均速度是:
. |
| v |
| (x1+x2+x3+x4+x5+x6) |
| 6T |
| (22.5+30+37.5+45+52.5+60)×10-3m |
| 0.6s |
(3)根据题意可知:△x=7.5mm,根据△x=aT2得:
a=
| △x |
| T2 |
| 7.5×10-3m |
| (0.1s)2 |
故答案为:(1)0.225,0.263;(2)0.187,0.413;(3)0.75.
点评:解决本题的关键掌握匀加速直线运动某段时间内的平均速度等于中间时刻的瞬时速度.以及掌握在相邻的相等时间内的位移之差是一恒量,△x=aT2.

练习册系列答案
相关题目
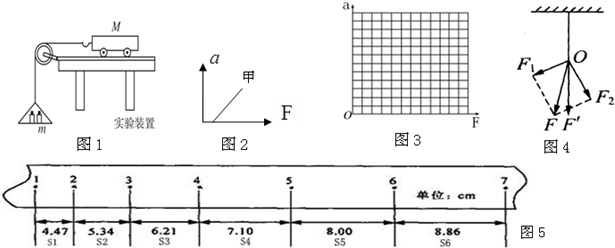

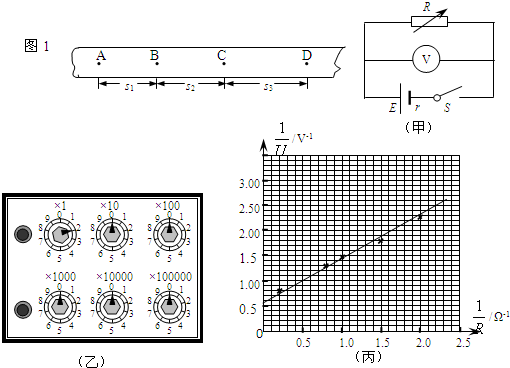
 某同学利用打点计时器测量小车做匀变速直线运动的加速度.
某同学利用打点计时器测量小车做匀变速直线运动的加速度.