题目内容
 据报道,2007年10月24日18时05分04.602秒我国的“嫦娥一号”卫星成功发射升空!圆了中国人几千年的梦想.我国整个探月工程分为“绕”、“落”、“回”3个阶段,第一期绕月工程就是通过发射探月卫星“嫦娥一号”,对月球表面环境、地貌、地形、地质构造与物理场进行探测.设嫦娥一号对月球进行科学探测时离月球表面的高度为h,周期为T,月球的半径为R,则
据报道,2007年10月24日18时05分04.602秒我国的“嫦娥一号”卫星成功发射升空!圆了中国人几千年的梦想.我国整个探月工程分为“绕”、“落”、“回”3个阶段,第一期绕月工程就是通过发射探月卫星“嫦娥一号”,对月球表面环境、地貌、地形、地质构造与物理场进行探测.设嫦娥一号对月球进行科学探测时离月球表面的高度为h,周期为T,月球的半径为R,则(1)月球的质量是多少?(用h、T、R表示)
(2)嫦娥探月计划以后将从月球表面采集样本送回地球,第一步是使月球登陆器离开月球表面绕月飞行,则能使登陆器离开月球表面所需的最小速度是多少?(用h、T、R表示)
分析:1、根据万有引力提供向心力G
=m(
)2(R+h),计算月球的质量M.
2、根据万有引力提供向心力G
=
,结合计算出来的月球的质量M,化简可得登陆器离开月球表面所需的最小速度.
| Mm |
| (R+h)2 |
| 2π |
| T |
2、根据万有引力提供向心力G
| Mm0 |
| R2 |
| mv02 |
| R |
解答:解:(1)设嫦娥一号的质量为m,月球的质量为M由万有引力定律可知嫦娥一号受月球的万有引力为
F万=G
=G
嫦娥一号所需的向心力为:F向=mω2r=m(
)2(R+h)
绕月飞行时万有引力等于所需的向力F万=F向
联立解得M=
(2)设登陆器的质量为m0,能使登陆器离开月球表面所需的最小速度为v
由万有引力定律可知登陆器在月球表面受月球的万有引力为
F万′=G
=G
登陆器有月球表面绕月飞行时所需的向心力为
F向′=
=
绕月飞行时万有引力等于所需的向力F万′=F向′
联立解得v=
答:(1)月球的质量是
;
(2)登陆器离开月球表面所需的最小速度是
.
F万=G
| Mm |
| r2 |
| Mm |
| (R+h)2 |
嫦娥一号所需的向心力为:F向=mω2r=m(
| 2π |
| T |
绕月飞行时万有引力等于所需的向力F万=F向
联立解得M=
| 4π2(R+h)3 |
| GT2 |
(2)设登陆器的质量为m0,能使登陆器离开月球表面所需的最小速度为v
由万有引力定律可知登陆器在月球表面受月球的万有引力为
F万′=G
| Mm |
| r2 |
| Mm0 |
| R2 |
登陆器有月球表面绕月飞行时所需的向心力为
F向′=
| mv2 |
| r |
| mv02 |
| R |
绕月飞行时万有引力等于所需的向力F万′=F向′
联立解得v=
| 2π(R+h) |
| T |
|
答:(1)月球的质量是
| 4π2(R+h)3 |
| GT2 |
(2)登陆器离开月球表面所需的最小速度是
| 2π(R+h) |
| T |
|
点评:解决本题的关键就是要掌握万有引力提供向心力这一关系,同时要能根据题目的要求熟练选择向心力的表达式.

练习册系列答案
相关题目
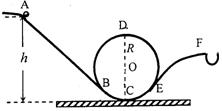
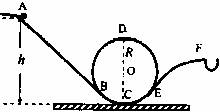
 (2008?佛山一模)在游乐园坐过山车是一项惊险、刺激的游戏.据《新安晚报》报道,2007年12月31日下午3时许,安徽芜湖方特欢乐世界游乐园的过山车因大风发生故障突然停止,16位游客悬空10多分钟后被安全解救,事故幸未造成人员伤亡.游乐园“翻滚过山车”的物理原理可以用如图所示的装置演示.斜槽轨道AB、EF与半径R=0.4m的竖直圆轨道(圆心为O)相连,AB、EF分别与圆O相切于B、E点,C为轨道的最低点,斜轨AB倾角为37°.质量为m=0.1kg的小球从A点静止释放,先后经B、C、D、E到F点落入小框.(整个装置的轨道均光滑,取g=10m/s2,sin37°=0.6,cos37°=0.8)求:
(2008?佛山一模)在游乐园坐过山车是一项惊险、刺激的游戏.据《新安晚报》报道,2007年12月31日下午3时许,安徽芜湖方特欢乐世界游乐园的过山车因大风发生故障突然停止,16位游客悬空10多分钟后被安全解救,事故幸未造成人员伤亡.游乐园“翻滚过山车”的物理原理可以用如图所示的装置演示.斜槽轨道AB、EF与半径R=0.4m的竖直圆轨道(圆心为O)相连,AB、EF分别与圆O相切于B、E点,C为轨道的最低点,斜轨AB倾角为37°.质量为m=0.1kg的小球从A点静止释放,先后经B、C、D、E到F点落入小框.(整个装置的轨道均光滑,取g=10m/s2,sin37°=0.6,cos37°=0.8)求: